Сил сопротивления

Расчетная модель может быть представлена рисунком 8 с условием, что демпфер 2 отсутствует.

Математически процесс колебания запишем дифференциальным уравнением второго порядка

.

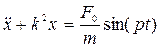Это уравнение можно вывести из уравнения Лагранжа II–го рода.

Обозначим

.

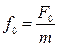Тогда дифференциальное уравнение вынужденных колебаний без учёта силы сопротивления

,

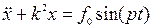где 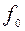– приведенная амплитуда возмущающей силы;

p – частота возмущающей силы;

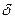– начальная фаза возмущающей силы.

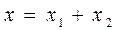Общее решение состоит из решения однородного уравнения и частного решения,

Известно, что общее решение однородного уравнения записывается как

,

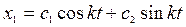а частное решение имеет вид

.

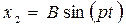Найдем амплитуду вынужденных колебаний В из уравнения

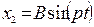
следующим образом

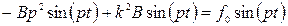, тогда амплитуда вынужденных колебаний

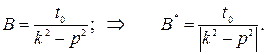
Общее уравнение принимает вид

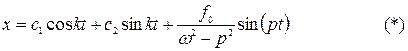
Для определения постоянных интегрирования дифференцируем уравнение (*)

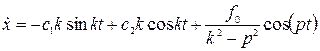
Подставляем начальные условия: 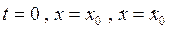в предыдущие уравнения и определяем постоянные интегрирования

.

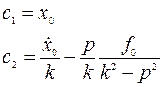Окончательно, закон колебания имеет вид

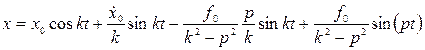
Биения – периодическое уменьшение и увеличение амплитуды суммарного сигнала - имеют место при близком значении частоты вынуждающей силы и частоты свободных колебаний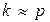

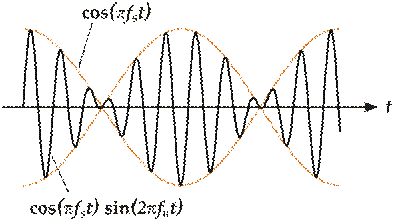
Рис.5. Биения

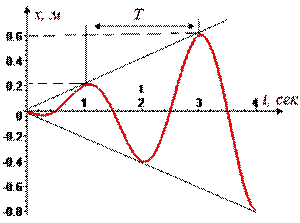
Рис.5. Резонанс

Резонанс – резкий рост амплитуды колебаний - будет наблюдаться при совпадении указанных частот

.

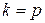При начальных условиях 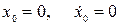имеем

,

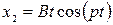тогда из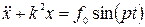

в результате преобразования получаем

;

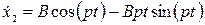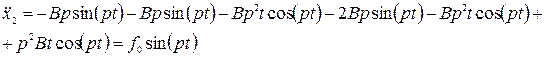Получаем ;

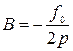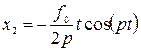– уравнение резонанса