Задание I
Модель процесса колебаний в общем виде показана на рисунке 8.
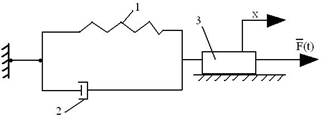
Рис. 1
Здесь обозначены:
1 – упругий элемент (моделируется в виде пружины);
с – коэффициент жёсткости упругого элемента;
2 – демпфер или гаситель колебаний;
b – коэффициент сопротивления возмущающей силе 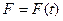 ;
;
3 – инерциальный элемент (материальная точка);
m – масса инерционного элемента (точки, тела).
В упругом элементе возникает сила упругости, которая на основании закона Гука определяется по формуле 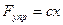 .
.
Сила сопротивления определяется по формуле: 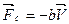 .
.
Основное уравнение динамики в векторном виде запишется как
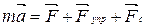 .
.
Спроецируем основное уравнение динамики на ось х
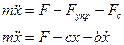 .
.
Перенеся в левую часть значения силы упругости и силы сопротивления, а затем, разделив на массу, получим
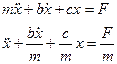 .
.
Обозначив 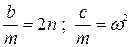 , имеем дифференциальное уравнение
, имеем дифференциальное уравнение
второго порядка с правой частью
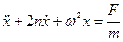 .
.
Различают:
● свободные колебания точки
a) 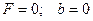 - свободные незатухающие колебания;
- свободные незатухающие колебания;
b) 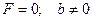 - свободные затухающие колебания;
- свободные затухающие колебания;
● вынужденные колебания точки
без учёта силы сопротивления;
b) 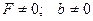 - вынужденные колебания
- вынужденные колебания
с учётом силы сопротивления.
1.1. Свободные колебания объекта
Свободными колебаниями называют колебания материального объекта, выведенного из состояния равновесия мгновенно приложенной к нему силой и процесс колебания в дальнейшем предоставлен самому себе.
Поскольку исследуется свободные колебания без учета сил сопротивления, то модель процесса колебания выглядит следующим образом
(рисунок 9).
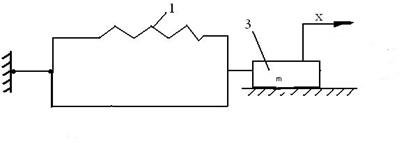
Рис. 2
Из определения свободных колебаний следует, что b= 0 и F = 0, тогда дифференциальное уравнение имеет вид
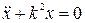 . (1)
. (1)
Уравнение (1) - дифференциальное уравнение свободных не затухающих колебаний (однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами).
Для решения уравнения (1) составляют характеристическое уравнение и определяют корни этого уравнения
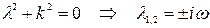 .
.
По корням уравнения решение дифференциального уравнения ищут в виде 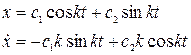 . (2)
. (2)
Поскольку постоянные с1 и с2 необходимо определить, то дифференцируем первое уравнение с целью соответствия количества уравнений количеству постоянных неизвестных.
Для определения постоянных величин необходимо знать начальные условия, т.е. при нулевом значении времени должны быть известны начальное смещение тела и начальное значение скорости
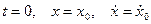 . (3)
. (3)
Подставляя (3) в (2), определяем постоянные интегрирования
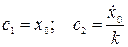 . (4)
. (4)
Подставив значения найденных констант в первое уравнение(2), имеем
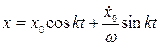 . (5)
. (5)
Уравнение (5) есть уравнение движения тела при свободных незатухающих колебаниях.
Если возникает необходимость определения амплитуды колебаний тела, то выразим постоянные интегрирования следующим образом
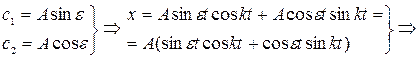
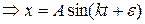 - гармоническое уравнение свободных незатухающих колебаний.
- гармоническое уравнение свободных незатухающих колебаний.
Возведя в квадрат левую и правую часть первоначального равенства и
складывая почленно, получим в результате преобразований амплитуду свободных незатухающих колебаний
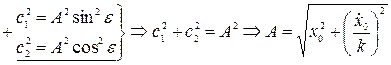 .
.
Определяем 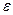 - начальную фазу колебаний:
- начальную фазу колебаний:
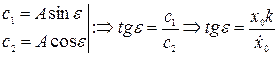 .
.
График свободных незатухающий колебаний - рисунок 3.
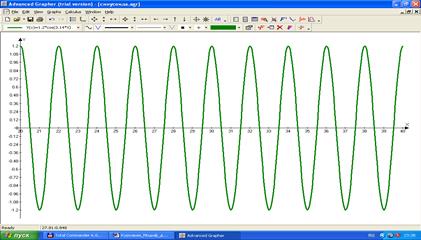
Рис. 3. Свободные колебания без трения
Максимальное значение колебаний 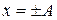 имеет место
имеет место
при 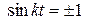 .
.
Важным параметром колебаний является Т – период свободных незатухающих колебаний. Т – временной интервал, через который точка, возвращается в исходное положение с той же скоростью и движется в том же направлением, т.е. на графике – это расстояние по оси t между двумя ближайшими точками, одинаково удаленными от оси х и имеющими одинаковые фазы колебаний.
Период колебаний можно вычислить по формуле
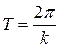 ,
,
так как период синуса равен 2p, а за период колебаний аргумент функции изменится на kT
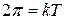 ,
,
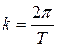 – круговая, или циклическая частота (собственная частота) колебаний.
– круговая, или циклическая частота (собственная частота) колебаний.
Принято оценивать колебания еще одним параметром
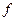 – техническая частота, число колебаний в 1 секунду
– техническая частота, число колебаний в 1 секунду
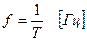 .
.
Подводя итог, уравнение (2) приводится к виду
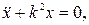
где 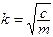 – частота свободных колебаний.
– частота свободных колебаний.
Общее решение уравнения, удовлетворяющее начальным условиям, равно
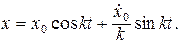
Период колебаний 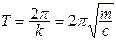 .
.
 2015-06-28
2015-06-28 1459
1459
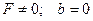 -
- 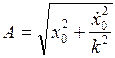 .
.