Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область.
Пусть на плоскости задача область G площади 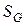 . В области G содержится область g площади Sg. В область G наудачу брошена точка. Будем считать, что брошенная точка может попасть в некоторую часть области G с вероятностью, пропорциональной площади этой части и не зависящей от ее формы и расположения. Пусть А – попадание брошенной точки в область g, тогда геометрическая вероятность этого события определяется формулой
. В области G содержится область g площади Sg. В область G наудачу брошена точка. Будем считать, что брошенная точка может попасть в некоторую часть области G с вероятностью, пропорциональной площади этой части и не зависящей от ее формы и расположения. Пусть А – попадание брошенной точки в область g, тогда геометрическая вероятность этого события определяется формулой
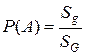 .
.
Аналогично вводится понятие геометрической вероятности при бросании точки в пространственную область G объема VG, содержащую область g объема Vg:
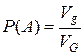 .
.
В общем случае понятие геометрической вероятности вводится следующим образом. Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки, брошенной наудачу в область g – часть области G, равна
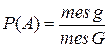
Пример 5.1. В круг вписан квадрат. В круг наудачу бросается точка. Какова вероятность того, что точка попадает в квадрат?
Обозначим: R – радиус круга, 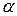 – сторона вписанного квадрата, А – попадание точки в квадрат, S – площадь круга, S1 – площадь вписанного квадрата.
– сторона вписанного квадрата, А – попадание точки в квадрат, S – площадь круга, S1 – площадь вписанного квадрата. 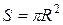 , а сторона вписанного квадрата через радиус вписанной окружности выражается формулой
, а сторона вписанного квадрата через радиус вписанной окружности выражается формулой 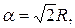 поэтому площадь квадрата
поэтому площадь квадрата 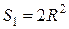 . Тогда искомая вероятность
. Тогда искомая вероятность
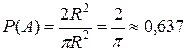
Пример 5.2. (Задача Бюффона). Плоскость расчерчена параллельными прямыми, расстояние между которыми равно 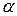 . На эту плоскость бросается наудачу отрезок длины
. На эту плоскость бросается наудачу отрезок длины  l(l <
l(l < 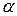 ) Какова вероятность того, что отрезок пересекается хотя бы с одной из прямых семейства?
) Какова вероятность того, что отрезок пересекается хотя бы с одной из прямых семейства?
 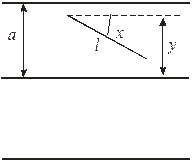 Рис. 1. Рис. 1. | Расстояние от верхнего конца отрезка до ближайшей снизу прямой обозначим через у (Рис. 1). Угол между отрезком и лучом, параллельным прямым семейства, начало которого совпадает с верхним концом отрезка, обозначим через х. Очевидно, что 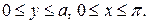 |
Для того, чтобы отрезок пересекал хотя бы одну из прямых семейства, необходимо и достаточно, чтобы у=а или 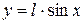 . Выражение «отрезок брошен наудачу» будем понимать так: точка (х, у) наудачу брошена на прямоугольник
. Выражение «отрезок брошен наудачу» будем понимать так: точка (х, у) наудачу брошена на прямоугольник 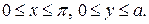 (Рис. 2).
(Рис. 2).
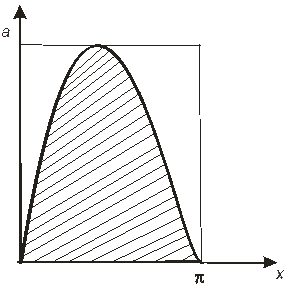 Рис. 2. Рис. 2. | Точки, координаты которых удовлетворяют неравенству 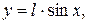 образуют фигуру, заштрихованную на Рис. 2. Площадь этой фигуры образуют фигуру, заштрихованную на Рис. 2. Площадь этой фигуры 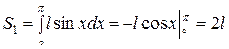 Площадь всего прямоугольника есть Площадь всего прямоугольника есть 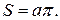 Тогда, если А – событие – отрезок пересекается хотя бы с одной прямой Тогда, если А – событие – отрезок пересекается хотя бы с одной прямой 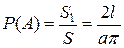 |
В случае l=a вероятность такова
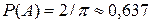
1. Как определяется геометрическая вероятность в плоском случае?
2. Как определяется геометрическая вероятность в пространственном случае?
3. Каковы свойства геометрической вероятности?
 2015-06-24
2015-06-24 2097
2097
