Статика твердого тела

2.2.1. Эквивалентные друг другу системы сил

Количество движения и кинетический момент твердого тела выражаются через скорость 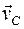полюса – центра масс и угловую

скорость 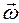тела (см. п. 3.2). Теоремы об изменении количества движения и об изменении кинетического момента дают возможность составить дифференциальные уравнения относительно проекций этих скоростей – дифференциальные уравнения движения тела. Количество этих уравнений равно числу степеней свободы тела. Главный вектор и главный момент системы внешних сил вполне определяют силовое влияние на тело со стороны окружающей среды. Поэтому системы сил, приложенные к твердому телу, считаются взаимно эквивалентными, если они имеют одинаковые главные векторы и главные моменты.

Пусть система сил состоит из одной силы. Перенеся силу вдоль линии ее действия, получим новую систему из одной силы, эквивалентную исходной. Таким образом, сила, приложенная к твердому телу, является скользящим вектором.

2.2.2. Векторные уравнения равновесия твердого тела

Если твердое тело покоится в течение некоторого промежутка времени, то меры механического движения его сохраняют в этом промежутке постоянные значения, равные нулю. Тогда из теорем динамики получаем необходимые условия равновесия твердого тела, накладываемые на приложенные к нему силы (уравнения равновесия системы сил):

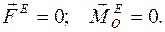
Внутренние силы на состояние твердого тела как единого объекта не влияют, поэтому индекс «Е» (Exterior) в записях уравнений равновесия по умолчанию опускают.

2.2.3. Классификация систем сил, действующих на твердое тело, по взаимному расположению линий их действия:

А) пространственные и плоские системы сил;

Б) сходящиеся системы сил (линии действия всех сил пересекаются в одной точке); системы параллельных сил (линии действия всех сил параллельны друг другу); произвольные системы сил.

Например: «пространственная система параллельных сил».

2.2.4. У равнения равновесия твердого тела (уравнения равновесия системы сил) в проекциях на оси декартовой системы координат

Уравнения равновесия произвольной пространственной системы сил

; ; ;

; ; .

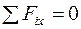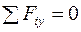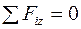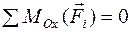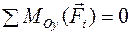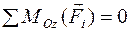Возможна краткая форма записи: 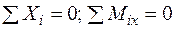и т.д.

Уравнения равновесия произвольной плоской системы сил

; ; .

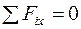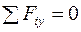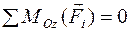В уравнении моментов для плоской системы сил индекс «z» по умолчанию опускают. Знаки моментов определяют по правилу часовой стрелки: если сила «стремится» повернуть плоскую фигуру вокруг данного полюса против часовой стрелки, то момент считают положительным, иначе – отрицательным. Если полюс лежит на линии действия силы, то момент равен нулю.

Можно составить уравнения равновесия плоской системы сил иначе:

- два уравнения моментов относительно разных полюсов и одно уравнение проекций сил на ось, не перпендикулярную прямой, содержащей полюсы;

- три уравнения моментов относительно трех разных полюсов, не лежащих на одной прямой.

2.2.5. Пара сил – система двух сил, равных по величине, направленных в противоположные стороны и имеющих не совпадающие линии действия. Главный вектор такой системы двух сил равен нулю, а главный момент относительно любого полюса есть один и тот же вектор 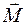, называемый моментом пары. Пусть 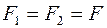; тогда величина момента пары равна 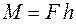. Здесь h – расстояние между линиями действия сил пары, называемое плечом пары (рис. 12).

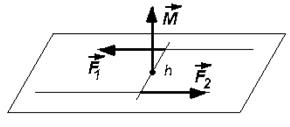
Рис. 12. Пара сил

Действие на твердое тело пары сил характеризуется действием на него силового момента 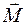. Силы, образующие пары, могут иметь те или иные величины, точки приложения и линии действия. Но если моменты этих пар одинаковы по величине и направлению, то такие пары эквивалентны друг другу. Момент пары сил – свободный вектор. Действие пары на тело часто изображают на рисунках ломаной линией со стрелками или круговой стрелкой.

2.2.6. Равнодействующая системы сил - это одна сила, эквивалентная данной системе сил. Если главный момент системы относительно полюса 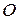оказался равен нулю, а главный вектор – нет, то говорят, что система сил приведена к равнодействующей. Так что если система сил имеет равнодействующую, то равнодействующая равна главному вектору системы.

2.2.7. Приведение системы сил к полюсу. Инварианты статики

Систему сил, приложенных к твердому телу, можно интерпретировать как совокупность приложенной в полюсе 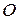силы, равной главному вектору 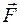, и пары, момент которой равен главному моменту 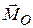. В этом смысле система сил считается приведенной к полюсу 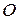. Главный вектор не зависит от полюса приведения, а главный момент при переходе от полюса О к полюсу С изменяется согласно формуле

,

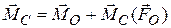где 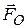- главный вектор, приложенный в полюсе .

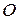При перемене полюса приведения сохраняет значение проекция 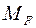главного момента на направление главного вектора. Величины 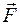и 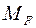называются инвариантами статики твердого тела.

Систему сил можно привести в общем случае к динаме; в частных случаях - к равнодействующей или к паре. Динама – это совокупность главного вектора и главного момента, в случае, когда они направлены вдоль одной прямой. Эта прямая называется осью динамы или центральной винтовой осью.

В случае равновесия системы сил главный вектор и главный момент относительно любого полюса равны нулю.

2.2.8. Центр тяжести тела - такая точка С выпуклого замыкания тела, через которую проходит линия действия равнодействующей сил тяжести при любом положении тела в пространстве. Если заданы веса 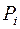фрагментов тела и координаты 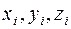центров тяжести этих фрагментов, то координаты общего центра тяжести С вычисляются по формулам:

; ; .

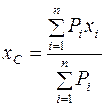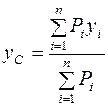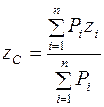Радиус-вектор центра масс: ,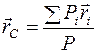

где 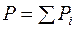- общий вес тела. Множители 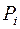в общем смысле называют весовыми коэффициентами. Выражения 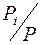называют нормированными весовыми коэффициентами, т.к. их сумма равна 1.

Координаты центра тяжести сплошного (континуального) тела, имеющего плотность 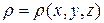: 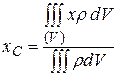, … и т.д.

Центр тяжести 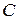фигуры, имеющей вид уголка (рис. 13), или бумеранга, находится вне уголка. Построив общую касательную к закруглениям его концов, получим выпуклую фигуру – выпуклое замыкание уголка, содержащее точку .

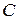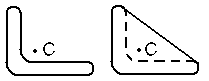
Рис. 13. Выпуклое замыкание плоской фигуры

2.2.9. Координаты центра тяжести однородного тела

А) Тело составлено из фрагментов:

.

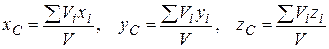Здесь роль весов играют объёмы (площади, длины) фрагментов. Если фрагмент представляет собой пустоту (раковину в теле), то его объём берется со знаком «-».

Б) Сплошное тело: , …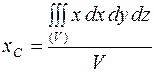

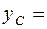В) Симметричное однородное тело: центр тяжести лежит в плоскости симметрии или на оси симметрии или совпадает с центром симметрии.

2.2.10. Теоремы Гюльдена

А) Пусть отрезок кривой 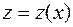, вращаясь вокруг оси Оz,

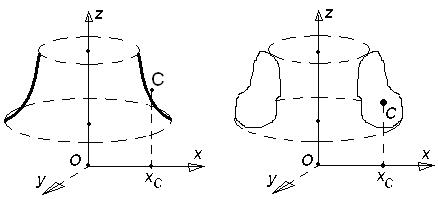
образовал поверхность вращения (рис. 14,а). Тогда площадь её

боковой части

,

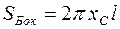где 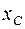- абсцисса центра С тяжести отрезка кривой, l - длина отрезка.

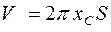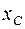Б) Пусть плоская фигура, вращаясь, образует тело вращения (рис. 14, б). Его объём равен , где - абсцисса центра тяжестифигуры, S – ее площадь.

а б

Рис. 14. Поверхность и тело вращения

2.2.11. Основные типы связей и их реакции

При решении задач на равновесие действие связей описывают, вводя в

задачу реакции связей и прикладывая их к выбранному объекту исследования.

После этого сами связи далее игнорируются (принцип освобождаемости от связей ) и объект считается условно свободным.

А) Связи в плоских задачах статики (рис.15)

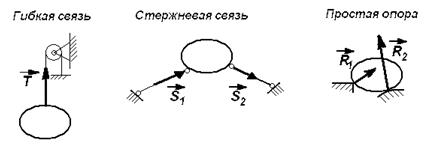
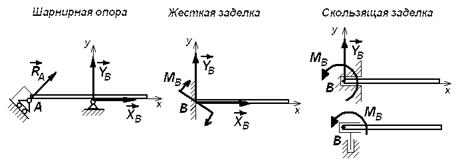
Рис. 15. Реакции связей в плоских задачах статики

Реакция гибкой связи направлена вдоль нити (каната, троса и т.п.) от объекта исследования.

Реакция невесомого стержня направлена вдоль прямой, соединяющей концы стержня. Стержень оканчивается шарнирами. Силы прикладываются к стержню только в его концах. Стержень или сжат, или растянут.

Реакция простой физически гладкой опоры направлена от опоры к объекту исследования вдоль нормали к их соприкасающимся поверхностям. Одна из этих поверхностей может быть геометрически не гладкой, если производные функций, задающих поверхность, имеют разрыв.

Реакция подвижной шарнирной опоры направлена перпендикулярно опорной поверхности. Эта опора выражает запрет на смещение конца А в направлении перпендикуляра к опорной поверхности и одновременно - разрешение на смещение конца А вдоль опорной поверхности и на поворот вокруг конца А.

Неподвижная шарнирная опора запрещает смещение точки В в плоскости 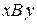и разрешает поворот вокруг В (т.е. вокруг оси шарнира). Направление реакции заранее не известно; при решении задачи искомую реакцию обычно раскладывают на составляющие 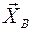и .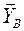

Жесткая заделка означает соединение балки со стеной, при котором все три степени свободы балки как плоской фигуры закрепощены. Действие заделки на балку характеризуется моментом заделки и составляющими силами.

Скользящая заделка оставляет закрепощённой «вращательную» степень свободы балки и одну или две поступательные; соответственно действие заделки на балку описывается моментом заделки и силой, перпендикулярной разрешенному направлению скольжения, или только моментом.

Б) В пространственных задачах встречаются:

цилиндрический шарнир, реакция которого описывается составляющими силами, перпендикулярными оси шарнира;

сферический шарнир, реакция которого описывается тремя составляющими силами;

заделка, реакция которой описывается в общем случае тремя составляющими силами и тремя составляющими момента заделки.

2.2.12. Статически определимые конструкции

Когда исследуют равновесие системы твердых тел, соединенных между собой тем или иным способом, то её называют конструкцией. Если неизвестные величины в задаче статики могут быть найдены из системы уравнений равновесия всей конструкции или ее частей, то конструкция называется статически определимой. Если число неизвестных больше числа уравнений статики, то конструкция будет статически неопределимой.

В задачах статики часто встречаются стержневые конструкции: фермы, рамы и проч. Стержнем называют цилиндрическое тело, поперечный размер которого мал по сравнению с размером в направлении образующей. Стержни могут «работать» не только на сжатие-растяжение, но и на изгиб и кручение; их в строительной механике называют также балками и брусьями. Рассмотрим плоскую конструкцию из трех стержней (балок) 1, 2 и 3, изображенную на рис. 16, а. На

каждый отдельно взятый в качестве твердого тела стержень действует плоская произвольная система сил (см. п. 2.2.4), и для трех стержней можно составить 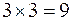уравнений равновесия. В этих уравнениях будут фигурировать 10 неизвестных реакций: реакции опор 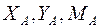и 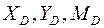, а также проекции действующих в шарнирах сил давления балок друг на друга: 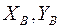и 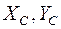(рис. 16,б). Количество неизвестных превышает число уравнений статики на 1; последнее число можно рассматривать как меру статической неопределимости данной конструкции. Найдем число степеней её свободы по формуле п. В.10. Система трех свободных балок как плоских фигур имеет 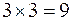степеней свободы. Уравнения связей, выражающие условия заделки:

; .

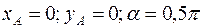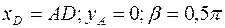Уравнения, описывающие шарнирные соединения балок друг с другом:

; .

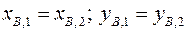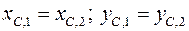Всего 10 уравнений связей; число степеней свободы

.

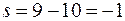Число степеней свободы статически определимой стержневой конструкции, изображенной на рис. 16, в, равно нулю.

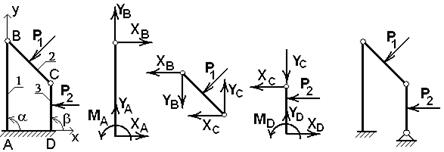
а б в

Рис. 16. Составные стержневые конструкции

Расчет статически неопределимой упругой стержневой конструкции выполняют методами сопротивления материалов. Допустив, что конструкция способна деформироваться, к уравнениям равновесия самой конструкции или ее частей как твердых тел добавляют уравнения, выражающие условия совместности деформаций ее частей. Систему уравнений равновесия замыкают уравнения, описывающие связь между деформациями и силами - закон упругости (закон Гука).