2.1.1.Аксиомы классической механики
А) Первый закон Ньютона (принцип инерции).
Б) Второй закон Ньютона в общем виде формулируется по отношению к материальной точке переменной массы
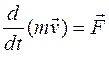 .
.
Основное уравнение динамики материальной точки постоянной массы:
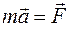 .
.
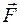 – сила, действующая на точку со стороны какого-то корпускулярного тела или силового поля (fors (лат.) – неодолимая сила, случай; fortis – сильный).
– сила, действующая на точку со стороны какого-то корпускулярного тела или силового поля (fors (лат.) – неодолимая сила, случай; fortis – сильный).
Второй закон Ньютона, как и другие уравнения динамики, формулируется («по умолчанию») относительно инерциальной системы отсчета (существование таких систем отсчета постулируется первым законом Ньютона). В качестве инерциальной системы берут обычно систему отсчета, связанную с Землей («геоцентрическая» система отсчета). С большей точностью второй закон Ньютона выполняется по отношению к системе отсчета, связанной с плоскостью эклиптики («гелиоцентрическая»), и еще точнее - относительно системы отсчета, связанной с «удаленными звездами».
В) Дополнение ко второму закону Ньютона (принцип независимости действия сил). Следствие: запись основного уравнения динамики точки в виде
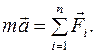
Г) Третий закон Ньютона (принцип соответствия действия и
противодействия): силы взаимодействия между материальными точками 1 и 2 связаны уравнением 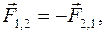 причем эти силы имеют общую линию действия, проходящую через точки 1 и 2.
причем эти силы имеют общую линию действия, проходящую через точки 1 и 2.
Простейшими следствиями законов Ньютона являются теоремы динамики. Они выражают связь между мерами механического движения и соответствующими им мерами действия сил. Теоремы динамики являются формами законов сохранения (импульса, момента импульса и энергии). Законы сохранения в свою очередь отражают свойства симметрии пространства и времени классической механики: однородность пространства, изотропность пространства, однородность времени.
2.1.2.Классификация сил, действующих на точки механической системы
А) Задаваемые («активные») силы и реакции связей.
Задаваемые – силы, действующие на точки исследуемой механической системы со стороны тех тел или силовых полей, которые непосредственно не ограничивают подвижность системы. Активная сила задается или непосредственно некой инструкцией, или указанием на какой-то физический закон (являющийся следствием не законов Ньютона, а иной физической теории).
Реакции связей - это силы, характеризующие действие связей на исследуемый объект. В задачах механики реакции связей обычно являются неизвестными величинами.
Б) Внешние и внутренние силы
Внешние силы (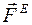 ; exterior (лат.) - внешний) – это силы, действующие на систему со стороны тех механических объектов, которые не входят в состав этой системы.
; exterior (лат.) - внешний) – это силы, действующие на систему со стороны тех механических объектов, которые не входят в состав этой системы.
Внутренние силы (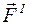 ; interior - внутренний) – это силы взаимодействия между фрагментами данной механической системы.
; interior - внутренний) – это силы взаимодействия между фрагментами данной механической системы.
Помимо вышеупомянутых двух основных способов классификации, в частных ситуациях применяют и иные. Так, например, силы, действующие на сплошное (континуальное) тело, подразделяются на объёмные и поверхностные, сосредоточенные силы и распределенные нагрузки.
2.1.3. Момент вектора относительно полюса (механический момент)
Момент вектора 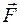 относительно полюса О определяется выражением
относительно полюса О определяется выражением
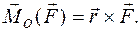
Здесь 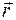 - радиус-вектор, проведенный из полюса О в точку приложения вектора
- радиус-вектор, проведенный из полюса О в точку приложения вектора  (рис. 9).
(рис. 9).
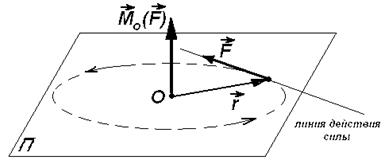
Рис. 9. Момент вектора 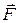
Латинское слово «момент» означает некое действующее начало, существенное качество какого-то явления. Момент силы характеризует вращательный эффект действия силы. Вектор момента силы направлен перпендикулярно плоскости П, содержащей полюс и линию действия силы 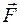 согласно правилу правого винта (линия действия силы – это прямая, вдоль которой направлен вектор силы).
согласно правилу правого винта (линия действия силы – это прямая, вдоль которой направлен вектор силы).
Величина момента силы равна произведению величины силы на плечо:
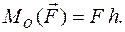
Плечо h вектора силы 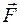 относительно полюса О – это расстояние от полюса до линии действия силы. Чтобы найти плечо, надо опустить из полюса перпендикуляр на линию действия силы.
относительно полюса О – это расстояние от полюса до линии действия силы. Чтобы найти плечо, надо опустить из полюса перпендикуляр на линию действия силы.
Аналогично определяется момент вектора 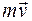 количества движения точки относительно полюса («кинетический момент»):
количества движения точки относительно полюса («кинетический момент»):
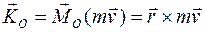 .
.
Пусть 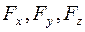 - декартовы проекции вектора
- декартовы проекции вектора 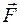 , а x, y, z - проекции радиус-вектора (то есть координаты точки приложения силы). Тогда момент вектора относительно начала координат
, а x, y, z - проекции радиус-вектора (то есть координаты точки приложения силы). Тогда момент вектора относительно начала координат
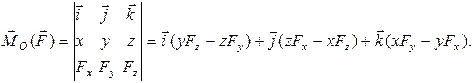 2.1.4. Момент вектора
2.1.4. Момент вектора 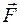 относительно оси
относительно оси 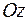
- это проекция момента относительно полюса О на ось Oz, проходящую через данный полюс:
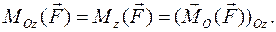
Чтобы найти момент вектора 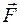 относительно оси Oz графо-аналитическим способом, воспользуемся следующим алгоритмом:
относительно оси Oz графо-аналитическим способом, воспользуемся следующим алгоритмом:
1) строим плоскость П (рис. 10), перпендикулярную оси Oz (точка О –точка их пересечения);
2) строим проекцию 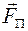 вектора
вектора 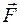 на плоскость П;
на плоскость П;
3) находим плечо 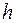 вектора
вектора 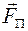 относительно полюса О и величину момента
относительно полюса О и величину момента 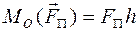 ;
;
4) Моменту вектора 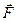 относительно оси Oz приписываем значение
относительно оси Oz приписываем значение
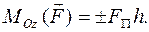
Знак момента определяется по правилу правого винта (часовой стрелки): если направление вектора 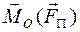 совпадает с направлением оси Oz, то «+», иначе «-».
совпадает с направлением оси Oz, то «+», иначе «-».
Рис. 10. Момент вектора  относительно оси
относительно оси
Момент вектора относительно оси равен нулю, если вектор и ось компланарны (линия действия вектора параллельна оси или пересекает её).
2.1.5.Главный вектор и главный момент системы сил
Множество сил  (i = 1,2,…, n), приложенных к точкам механической системы, называют системой сил.
(i = 1,2,…, n), приложенных к точкам механической системы, называют системой сил.
Главный вектор системы сил: 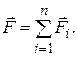
Главный момент системы сил относительно данного полюса О:
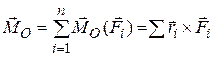 .
.
Главный вектор и главный момент системы внутренних сил равны нулю (следствие третьего закона Ньютона).
2.1.6. Меры механического движения
А) Количество движения материальной точки 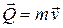 .
.
Количество движения механической системы, состоящей из n точек:
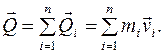
Количество движения механической системы можно найти как произведение общей массы системы на скорость центра масс (см. далее).
Б) Кинетический момент материальной точки относительно неподвижного полюса О (момент количества ее движения относительно полюса):
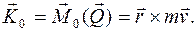
Кинетический момент механической системы относительно полюса О
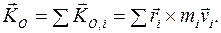
В) Кинетическая энергия материальной точки
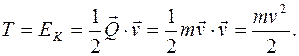
Кинетическая энергия механической системы
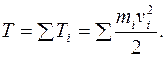
Формулы для мер механического движения механической системы выражают существенное свойство меры множества – ее аддитивность (мера движения механической системы есть сумма мер движения фрагментов системы).
2.1.7. Меры действия сил
А) Импульс силы
Элементарный импульс силы (импульс действия силы за бесконечно малое время dt): 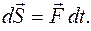
Суммарный элементарный импульс множества сил, приложенных к точкам механической системы:
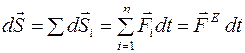 ,
,
где 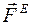 - главный вектор системы внешних сил.
- главный вектор системы внешних сил.
Импульс силы 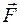 за промежуток времени
за промежуток времени 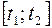 равен
равен
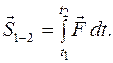
Б) Момент силы относительно полюса или оси (см. п. 2.1.4)
В) Работа и мощность силы
Элементарная работа силы 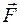 на бесконечно малом перемещении
на бесконечно малом перемещении 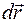 точки приложения силы - скалярное произведение векторов
точки приложения силы - скалярное произведение векторов 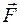 и
и 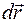 :
:
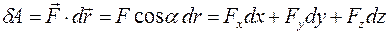 ,
,
где 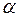 - угол между векторами
- угол между векторами 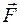 и
и 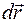 .
.
Работа на «конечном» перемещении точки из положения 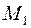 на траектории в положение
на траектории в положение 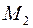 есть криволинейный интеграл второго рода:
есть криволинейный интеграл второго рода:
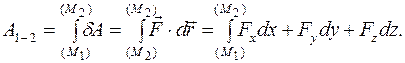
Мгновенная мощность силы 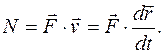
Если элементарная работа, то есть является полным дифференциалом функции работы: 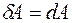 , то
, то 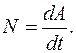 Мощность, силы как и работа, является скалярной величиной. Она может быть положительна, отрицательна или равна нулю.
Мощность, силы как и работа, является скалярной величиной. Она может быть положительна, отрицательна или равна нулю.
2.1.8. Мощность и элементарная работа сил, действующих на твердое тело
Суммарная мощность всех сил, действующих на тело, равна
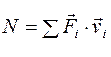 .
.
Скорость i –ой точки тела в общем случае его движения (см. п. 1.5.5):
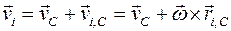 ,
,
где 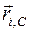 - радиус-вектор
- радиус-вектор 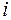 -ой точки относительно полюса С (рис. 11).
-ой точки относительно полюса С (рис. 11).
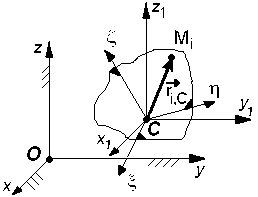
Рис. 11. Центр масс
Суммарная мощность сил будет равна
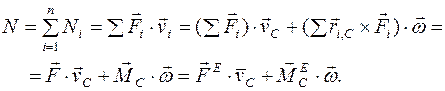
Определим вектор бесконечно малого поворота тела как 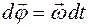 ; тогда суммарная элементарная работа сил
; тогда суммарная элементарная работа сил
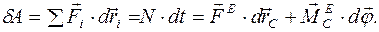
Поскольку главный вектор и главный момент внутренних сил равны нулю, то эти силы не совершают работы при движении твердого тела. Работа складывается из работы главного вектора внешних сил при поступательном движении тела (вместе с полюсом С) и работы главного момента внешних сил при сферическом движении вокруг полюса.
При вращательном движении тела вокруг неподвижной оси 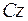 , проходящей через полюс
, проходящей через полюс 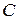 , суммарная элементарная работа сил равна
, суммарная элементарная работа сил равна 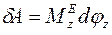 , а мощность сил
, а мощность сил 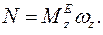
2.1.9.Теоремы динамики механической системы в дифференциальной форме можно записать как суждения о скоростях изменения мер движения:
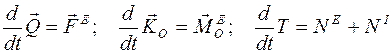 .
.
(Подчеркнем, что скорость изменения кинетической энергии есть суммарная мощность внешних и внутренних сил!)
 2015-06-28
2015-06-28 2812
2812
