Кванторы

В программировании квантор определяется как логический оператор, с помощью которого по предикату строится высказывание относительно области истинности предиката.

Пусть Р(х) – предикат, определенный на М, т. е. 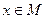. Тогда под высказыванием «для всех х из М Р(х) истинно» мы понимаем высказывание, которое является истинным, если Р(х) истинно для любого х. Высказывание записанное в кавычках обозначается 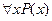, множество М не входит в обозначение, но должно быть ясно из контекста. Знак 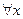, называется квантором общности.

А под высказыванием «существует такой х их М, что Р(х) истинно» мы понимаем высказывание, которое является истинным, если найдется хотя бы один х такой, что Р(х) является истинным. Высказывание в кавычках обозначается 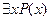. Знак 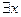, называется квантором существования.

Переход от Р(х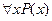) к или к 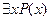называется связыванием переменной х (или квантификацией). Переменная, на которую навешан квантор, называется связанной, несвязанная переменная называется свободной.

Квантору общности соответствует связывание словами «для всех», квантору существования – словом «существует».

Навешивать кванторы можно и на многоместные предикаты. Выражение, на которое навешивается квантор общности или квантор сущности, называется областью действия квантора. Навешивание квантора на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных. Это обуславливается определением смысла связанных и свободных переменных. Свободная переменная – это обычная переменная, которая может принимать различные значения из М, а выражение Р(х) – переменное высказывание, зависящее от значения х. Выражение 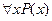не зависит от переменной х и при фиксированных М и Р имеет определенное значение. Это означает, что переход от 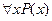к 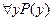не меняет истинности выражения.

Пример кванторов:

Пусть Р(х) – предикат, х – четное число, тогда высказывание 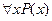- истинно на любом множестве четных чисел и ложно на множестве, содержащем хотя бы одно нечетное число. Высказывание 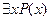- истинно на любом множестве, содержащим хотя бы одно четное число и ложно на любом множестве нечетных чисел.