2015-06-28
183
Известно, что поверхность G в R3 задается либо неявно уравнением G(x,y,z)=0, либоявно уравнениями
(1) x=gх(y,z), (2) y=gу(x,z), (3) z=gz(x,y), причемсоответствующие функции g двух переменных определены
в областях Sxy, Sxz, Szy - проекциях поверхности G на координатные плоскости XOY, XOZ, YOZ.
Например,сфера G:x2+y2+z2=1 ó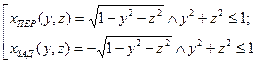 
- уравнения передней и задней полусфер.
Известно, что гладкая поверхность имеет в точке М€ G касательную плоскость aКАС и нормаль LN,
которая называется «нормалью к поверхности в точке»:
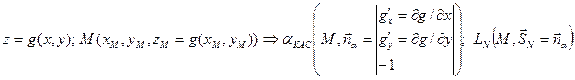
Координатами единичного вектора нормали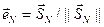 
; 
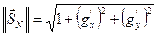являются его «направляющие косинусы» eN=[cos(a);cos(b);cos(g)] t, где a,b,g- углы между вектором нормали в точке и ортами соответствующих координатных осей прямоугольной системы координат.
-------------------------------------------------------------------------------------------------------------------------------------------------------------
Пусть GV - гладкая поверхность в R3, проекции которой на координатные плоскости обозначим Sxy, Sxz, Szy.
Выделим в окрестности точки М бесконечно малую ячейку поверхности d σ. Ее проекции на координатные плоскости будут равны, соответственно:
|
|
|
d σXOY= dSxy=d σ∙|cos(a)|; d σXOZ= dSxz= d σ∙|cos(b)|; d σYOZ= dSzy=d σ∙|cos(g)|
Пусть в замкнутой области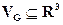 
задано непрерывное векторное поле
F (r) =[ Fx(r);Fy(r);Fz(r) ] t
Проекция поля на нормаль LN к поверхности G в точке M (r) равна
ПРNF (r) =(F●eN)=Fxcos(a)+Fycos(b)+Fzcos(g).
