Теорема: Квадратичная форма 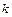 является положительно определенной
является положительно определенной 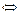 в некотором (любом) базисе все главные миноры матрицы квадратичной формы являются положительными. Квадратичная форма
в некотором (любом) базисе все главные миноры матрицы квадратичной формы являются положительными. Квадратичная форма 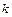 является отрицательно определенной
является отрицательно определенной 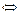 в любом базисе главные миноры четного порядка матрицы квадратичной формы положительны, а главные миноры нечетного порядка – отрицательны.
в любом базисе главные миноры четного порядка матрицы квадратичной формы положительны, а главные миноры нечетного порядка – отрицательны.
Без доказательства.
Определение: главные миноры матрицы – миноры, получающиеся вычеркиванием последних строк и столбцов.
Замечание: Пусть 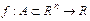 и
и 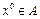 . Матрица квадратичной формы второго дифференциала
. Матрица квадратичной формы второго дифференциала 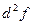 (или матрица Гессе) в точке
(или матрица Гессе) в точке 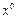 имеет вид:
имеет вид: 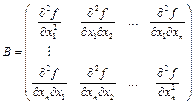
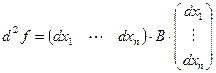 в точке
в точке 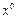 .
.
Теорема: (о равенстве смешанных производных)
Пусть 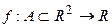 и
и 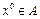 . Пусть
. Пусть 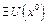 такая, что
такая, что 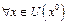 существует непрерывные
существует непрерывные 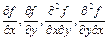 . Тогда
. Тогда 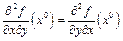 .
.
Доказательство: Возьмем 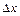 и
и 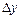 такие, что
такие, что 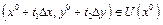 ,
, 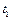 и
и 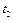 такие, что
такие, что 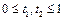 .
.
Рассмотрим следующее выражение: 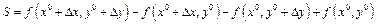 . Обозначим
. Обозначим 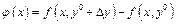 ,
, 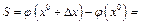 (т.к.
(т.к.  дифференцируема,
дифференцируема, 
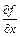 по теореме Лагранжа
по теореме Лагранжа 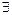
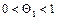 такая, что)
такая, что) 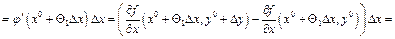 (т.к. функция
(т.к. функция 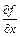 дифференцируема по
дифференцируема по 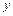 , по теореме Лагранжа
, по теореме Лагранжа 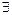
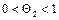 такая, что)
такая, что) 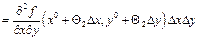 . Аналогично рассмотрим функцию
. Аналогично рассмотрим функцию 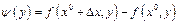 , получаем, что
, получаем, что 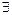
 такие, что
такие, что 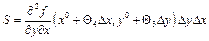 .
.
Таким образом, получаем
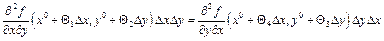 . Переходя к пределу при
. Переходя к пределу при  и
и  , получаем, в силу непрерывности
, получаем, в силу непрерывности 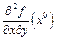 и
и 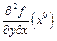 , что
, что 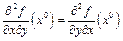 . <
. <
Контрпример: Рассмотрим
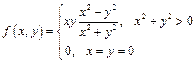
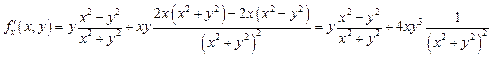 ,
,
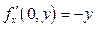 ;
; 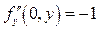
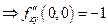
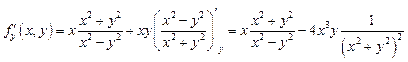
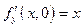 ;
; 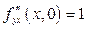 и
и 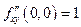
Таким образом, 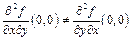 .
.
 2015-06-28
2015-06-28 199
199







