Производные и дифференциалы высших порядков

Определение: частной производной порядка 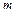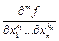в точке 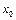называется 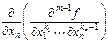, где .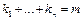

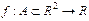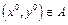Определение: Пусть и . Дифференциалом второго порядка называется выражение вида: .

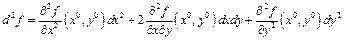Замечание: Дифференциал второго порядка является квадратичной формой на приращениях.

(Выделенное жёлтым спрашиваться не будет. Зелёным выделено самое важное.)

Определение: Пусть 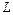- линейное пространство. Билинейной формой (функцией) называется функция 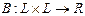такая, что 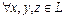и :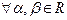

1)

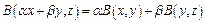
2)

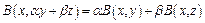
Определение: билинейная форма называется симметричной, если .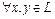

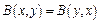Пример: скалярное произведение векторов – симметричная билинейная форма.

Определение: квадратичной формой называется 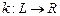такая, что симметричная билинейная форма , для которой .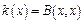

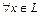Замечание: симметричная билинейная форма однозначно восстанавливается по ее квадратичной форме: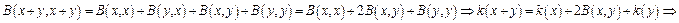

.

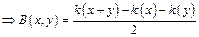Определение: квадратичная форма 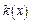называется положительно определенной, если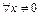 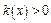; квадратичная форма 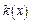называется отрицательно определенной, если .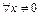

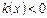Определение: Пусть 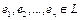- базис в 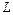. Тогда квадратичная форма в этом базисе имеет матрицу 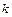. Закон преобразования матрицы 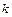при переходе к новому базису: 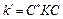, где 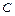- матрица перехода к новому базису.