Опр.: Пусть 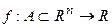 ,
, 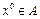 и
и 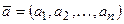 некоторый вектор
некоторый вектор 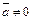 . Производной функции
. Производной функции 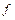 по вектору
по вектору 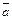 в точке
в точке 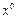 называется число:
называется число:
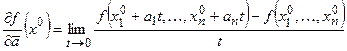 , если оно существует.
, если оно существует.
Замечание: если 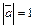 , то производная по вектору является производной по направлению.
, то производная по вектору является производной по направлению.
Частные производные 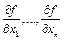 являются производными по векторам
являются производными по векторам 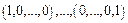 .
.
Опр.: Пусть 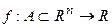 ,
, 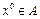 и
и 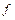 имеет все частные производные в точке
имеет все частные производные в точке 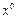 . Градиентом функции
. Градиентом функции 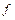 в точке
в точке 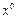 называется вектор
называется вектор 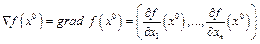 .
.
Теорема: Пусть 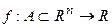 ,
, 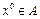 и
и 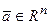 . Тогда
. Тогда 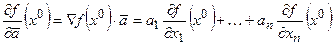 .
.
Без док-ва.
Замечание: Если функция имеет все производные по векторам, из этого не следует дифференцируемость.
Опр.: Пусть 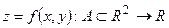 и
и 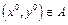 . Касательной плоскостью к графику функции
. Касательной плоскостью к графику функции 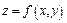 в точке
в точке 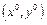 называется плоскость, заданная уравнением
называется плоскость, заданная уравнением 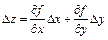 или
или
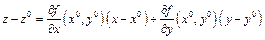 .
.
Если имеется функция 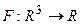 и уравнение
и уравнение 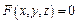 и в точке
и в точке 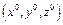 , такой что
, такой что 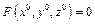 касательная плоскость к графику функции
касательная плоскость к графику функции 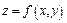 имеет вид:
имеет вид:
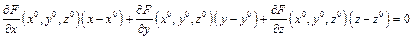 .
.
 2015-06-28
2015-06-28 224
224







