1. У векторному просторі 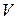 існує єдиний нульовий вектор,
існує єдиний нульовий вектор, 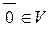 .
.
2. Кожний вектор 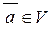 у векторному просторі має єдиний протилежний вектор
у векторному просторі має єдиний протилежний вектор 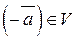 .
.
Аксіоми операції множення на скаляр
Розглянемо властивості операції множення вектора на скаляр у векторному просторі:
1. Якщо 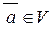 і
і 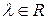 , то
, то 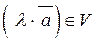 .
.
2. 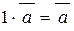 . 3.
. 3. 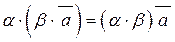 , де
, де 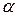 і
і 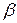 – деякі дійсні числа.
– деякі дійсні числа.
4. 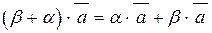 . 5.
. 5. 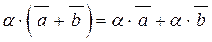 .
.
6. При множенні будь-якого вектора векторного простору, 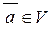 на число нуль
на число нуль 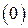 одержуємо нуль-вектор,
одержуємо нуль-вектор, 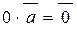 .
.
7. Протилежний вектор 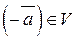 можна представити як добуток самого вектора
можна представити як добуток самого вектора 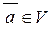 на число
на число 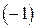 ,
, 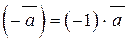 .
.
Операція віднімання
Існування протилежних векторів у векторному просторі 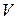 дозволяє ввести операцію віднімання як обернену до операції додавання
дозволяє ввести операцію віднімання як обернену до операції додавання
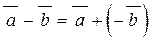 .
.
 2015-06-28
2015-06-28 201
201







