Лінійні операції над векторами зводяться до лінійних операцій над їх координатами.
1. Д о д а в а н н я в е к т о р і в. Координати суми векторів 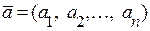 ,
, 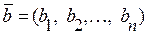 дорівнюють сумі відповідних координат
дорівнюють сумі відповідних координат
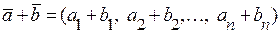 .
.
2. В і д н і м а н н я в е к т о р і в. Координати різниці векторів 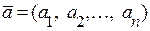 ,
, 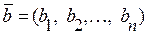 дорівнюють різниці відповідних
дорівнюють різниці відповідних
координат
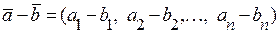 .
.
3. М н о ж е н н я в е к т о р а н а ч и с л о. Координати добутку вектора 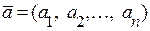 на число
на число 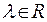 дорівнюють добутку координат вектора
дорівнюють добутку координат вектора 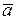 на це число
на це число
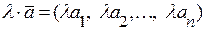 .
.
Всі розглянуті лінійні операції з векторами заданими координатами задовольняють аксіоми лінійного простору 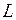 .
.
Аксіоми операції додавання
Розглянемо властивості операції додавання у векторному просторі:
1. Якщо 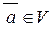 і
і 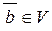 , то
, то 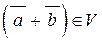 .
.
2. 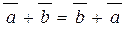 . 3.
. 3. 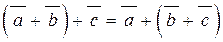 .
.
4. Існує нульовий вектор 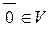 (нуль-вектор), який при додаванні не змінює вектори векторного простору
(нуль-вектор), який при додаванні не змінює вектори векторного простору 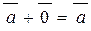 .
.
5. Для кожного вектора векторного простору, 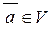 , існує протилежний вектор
, існує протилежний вектор 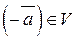 , при додаванні якого одержують нуль-вектор
, при додаванні якого одержують нуль-вектор 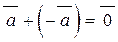 .
.
 2015-06-28
2015-06-28 214
214








