Тема 3. Матричные модели

Балансовый метод планирования, матричные модели. Экономико-математическая модель межотраслевого стоимостного баланса, определение объемов валовой и конечной продукции. Матрица коэффициентов прямых материальных затрат, ее продуктивность. Признаки продуктивности. Матрица коэффициентов полных материальных затрат, способы ее определения. Межпродуктовый баланс. Примеры использования матричных моделей, сведения о компьютерной реализации.

Литература: /1, глава 6/; /3, раздел 1.5/

Матричные (балансовые) модели представляют собой математическое выражение балансового метода планирования - метода взаимного сопоставления затрат и результатов (метод «затраты-выпуск»).

Матричные модели обьединяет общий принцип построения, единство системы расчетов и аналогичность ряда экономических характеристик.

Рассмотрим применение балансового метода планирования на примере матричной модели межотраслевого баланса.

Предположим, что на некоторый период времени (например, год) планируется деятельность экономической системы, состоящей из 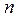отраслей.

Введем обозначения, пусть:

X = (Х_1, Х_2,….,,Х_n) - вектор валовой продукции (X_i – общий объем производства отрасли i за рассматриваемый период);

Y = (Y_1,Y_2,….,Y_n) - вектор конечной продукции (Y_i – конечный продукт отрасли i, т.е.продукт выходящий за пределы рассматриваемой системы);

Х_ij - производственные (материальные) затраты j -й отраслью продукции i -й отрасли в течение планового периода (например, если отрасль 1 - угольная, отрасль 2 - черная металлургия, то Х₁₂ - годовые затраты угля на производство черных металлов). Это межотраслевые потоки – они характеризуют внутреннее потребление продукции.

Единицы измерения всех указанных величин могут быть или натуральными (т, пог.м и т.п.) или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевые балансы. Ниже рассматривается стоимостной баланс.

ЭММ межотраслевого баланса (МОБ) разрабатывается на основе метода «затраты-выпуск» и представляет собой систему уравнений, отражающих функциональную взаимосвязь включенных в его систему элементов:

……………………………….

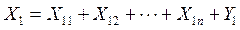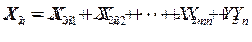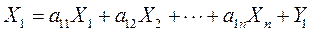С учетом обозначений а_{i j} = Х_{i j} / Х_j; Х_{i j} = а_{i j} Х_j система уравнений МОБперепишется в виде:

………………………………..

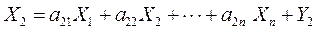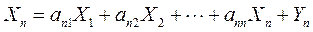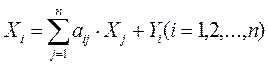или в более компактном виде:

(запись с использованием знаков суммирования),

X = AX +Y, где A = (а_{i j})_n*n; X, Y- матрицы-столбцы.

(запись в матричной форме).

Именно в этих двух формах записи, как правило, и используется ЭММ межотраслевого баланса. Эту модель называют еще моделью Леонтьева или моделью "затраты - выпуск".

Элементы а_ij матрицы А называют коэффициентами прямых (материальных) затрат - это затраты продукции i -й отрасли на единицу (например, на один рубль) валовой продукции j - ой отрасли.

В матричной форме модель Леонтьева можно записать в виде X-AX=Y или (E-A)X=Y (E – единичная матрица ).

Последнее соотношение можно использовать для анализа и планирования и решать следующие задачи:

1) Определить объемы конечного продукта отраслей Y_1, Y_2…. Y_n по заданным объемам валовой продукции - Y= (E-A)X.

2)

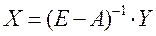Определить объемы валовой продукции отраслей X_1, X_2…. X_n по заданным объемам конечной продукции -

или X=BY, где B= (E-A)^-1.

3) Кроме того, можно определить величины конечной продукции части отраслей и объемы валовой продукции других отраслей, если задать для первых отраслей величины валовой продукции, а для всех остальных отраслей задать объемы конечной продукции.

Элементы b_ij обратной матрицы B=(E-A)^-1 называются коэффициентами полных (материальных) затрат - это затраты продукции i - й отрасли на единицу (например, на один рубль) конечной продукции отрасли j.

Соответственно, матрицу B называют матрицей коэффициентов полных затрат, а матрицу А - матрицей коэффициентов прямых затрат.

Обычно результаты балансовых расчетов приводят в следующей таблице стоимостного баланса:

Отрасли- Отрасли- потребители производители			.…	n	Конечный продукт	Валовой продукт
			….
			….
…..	…	…	….	...	......	…..
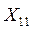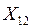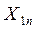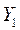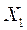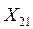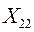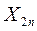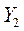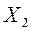n			….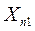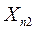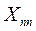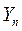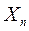
Условно чистая продукция			….			_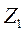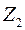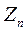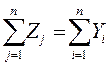
Валовой продукт			….		_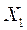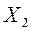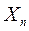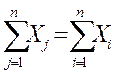

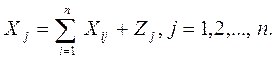Рассматривая схему баланса по столбцам, можно заметить, что итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции равен валовой продукции этой отрасли. Данный вывод можно записать в виде соотношения:

Величина условно чистой продукции 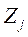равна сумме амортизации, оплаты труда и чистого дохода отрасли j. Приведенное выше соотношение охватывает систему из n уравнений, отражающих стоимостной состав продукции всех отраслей материальной сферы.

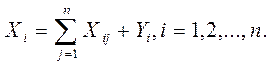Рассматривая схему МОБ по строкам для каждой производящей отрасли, видим, что валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих ее продукцию отраслей и конечной продукции данной отрасли:

Балансовый характер таблицы МОБ выражается в том, что:

, .

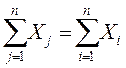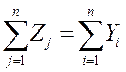Пример. Построить модель МОБ для трех отраслей по следующим данным:

А = 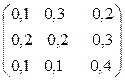, Y =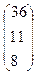

Произвести балансовые расчеты, результаты представить в табличной форме.