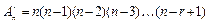 (1)
(1)
Доказательство. 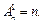 Перейдем к нахождению
Перейдем к нахождению 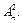
Мы имеем (n – 1) размещений, в которых на первом месте стоит первый элемент; (n – 1) размещений, в которых на первом месте стоит второй элемент; (n – 1) размещений, в которых на первом месте стоит третий элемент, 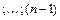 размещений, в которых на первом месте стоит n -й элемент, т.е.
размещений, в которых на первом месте стоит n -й элемент, т.е. 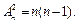 Возникает гипотеза, что
Возникает гипотеза, что
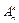 = n (n – 1)(n – 2)(n – 3)... (n – k +1).
= n (n – 1)(n – 2)(n – 3)... (n – k +1).
Перейдем к нахождению 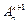 при такой гипотезе. Каждое размещение из n по
при такой гипотезе. Каждое размещение из n по 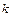 может дать
может дать 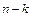 размещений из n по
размещений из n по 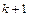 , после присоединения одного из объектов, не вошедших в него, отсюда
, после присоединения одного из объектов, не вошедших в него, отсюда
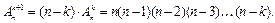 ■
■
2. Перестановкой n -й степени называется взаимное расположение n элементов относительно друг друга, т.е. размещение из n по n. Число всех различных перестановок n -й степени обозначается через 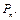 Тогда
Тогда 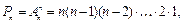 т.е.
т.е.
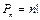 (2)
(2)
В новых обозначениях формулу (1) можно переписать в виде 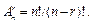 Договоримся также, что
Договоримся также, что 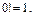
 2015-06-28
2015-06-28 348
348








