Сочетанием из n по r называется неупорядоченная выборка объема r из n элементов, т.е. любое подмножество, состоящее из r элементов, взятых из множествa n элементов. Число всех различных сочетаний из n по r обозначается 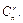 Заметим, что
Заметим, что 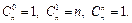
ТЕОРЕМА (правило симметрии). 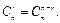 (1)
(1)
Доказательство. Выбор r элементов равносилен отбору 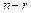 элементов, не включаемых в выборку. ■
элементов, не включаемых в выборку. ■
ТЕОРЕМА (формула Паскаля). 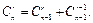 (2)
(2)
Доказательство. Фиксируем один из объектов. Все сочетания разбиваются на два класса: класс сочетаний, не содержащих фиксированный элемент (в нем 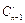 сочетаний), и класс сочетаний, содержащих фиксированный элемент (в нем
сочетаний), и класс сочетаний, содержащих фиксированный элемент (в нем 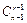 сочетаний). Отcюда и следует формула Паскаля. ■
сочетаний). Отcюда и следует формула Паскаля. ■
Значения 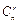 могут быть последовательно записаны с помощью этой формулы в треугольник Паскаля
могут быть последовательно записаны с помощью этой формулы в треугольник Паскаля
0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1
5 1 5 10 10 5 1
6 1 6 15 20 15 6 1
7 1 7 21 35 35 21 7 1
n 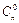
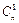
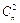
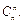
Выбрать r из n разных объектов можно 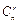 способами. Имеется r! возможностей упорядочить объекты каждого сочетания. Согласно правилу умножения имеется r!
способами. Имеется r! возможностей упорядочить объекты каждого сочетания. Согласно правилу умножения имеется r! 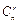 возможностей выбрать и разместить по r разным местам r из n разных объектов, т.е.
возможностей выбрать и разместить по r разным местам r из n разных объектов, т.е. 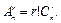 Отсюда
Отсюда
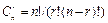 (3)
(3)
или
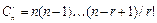 (4)
(4)
 2015-06-28
2015-06-28 243
243








