Упорядоченная выборка, в которой элементы могут повторяться, называется размещением с повторениями. Число всех размещений с
повторениями из n пo r будем обозначать 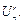 По определению
По определению 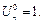
ТЕОРЕМА. 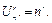
Доказательство проведем методом полной математической индукции по переменной r. Очевидно, что 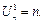 Предположим, что для
Предположим, что для 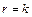 справедливо равенство
справедливо равенство 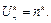 Пусть
Пусть 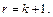 С помощью правила умножения можно доказать равенство
С помощью правила умножения можно доказать равенство
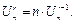 (1)
(1)
Отсюда 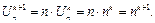 ■
■
ТЕОРЕМА. Число всех подмножеств конечного множества 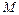 из n элементов равно
из n элементов равно 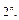
Доказательство. Выберем подмножество. Если элемент принадлежит подмножеству, то кодируем эту ситуацию символом 1, а если не принадлежит, то символом 0. Элементы исходного множества пронумеруем. Тогда каждому подмножеству ставится во взаимнооднозначное соответствие размещение с повторениями из двух элементов 0 и 1 по n. Таких размещений 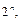 поэтому и подмножеств
поэтому и подмножеств 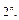 ■
■
С другой стороны, таких подмножеств 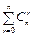 и, тем самым, формула (3) из предыдущего параграфа доказана вторым способом.
и, тем самым, формула (3) из предыдущего параграфа доказана вторым способом.
 2015-06-28
2015-06-28 225
225








