Упражнения. 1. Взять произвольно функцию, проверить, является ли она несамодвойственной

1. Взять произвольно функцию, проверить, является ли она несамодвойственной. Если функция несамодвойственная, то с помощью алгоритма, описанного в доказательстве леммы о несамодвойственной функции, построить константу.

2. Взять произвольно функцию, проверить, является ли она немонотонной. Если функция немонотонная, то с помощью алгоритма, описанного в доказательстве леммы о немонотонной функции, построить отрицание.

3. Взять произвольно функцию, проверить, является ли она нелинейной. Если функция нелинейная, то с помощью алгоритма, описанного в доказательстве леммы о нелинейной функции, построить конъюнкцию или отрицание конъюнкции.

4.7. Теорема Поста о функциональной полноте

ТЕОРЕМА (критерий полноты функциональной системы). Для полноты функциональной системы необходимо и достаточно, чтобы для каждого из пяти важнейших замкнутых классов в ней нашлась функция, ему не принадлежащая.

Доказательство. Þ Пусть N – полный класс и N Í Т ₀ Þ [ N ] Í [ Т ₀] Þ Р ₂ Í Т ₀ Þ Р ₂ = Т ₀.Противоречие. Следовательно, в классе N найдется функция, не сохраняющая константу 0. Аналогично приходим к противоречию, предположив, что полный класс N принадлежит классам T _1, L, M, S.

Ü Предположим, что в классе N найдутся функции f ₀ Ï Т ₀, f ₁Ï T ₁, f ₂ Ï S,

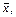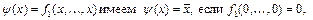
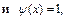
f ₃ Ï M, f ₄ Ï L. Так как f ₀(0,…, 0) = 1, то j (x) = f ₀(x, …, x) = если f ₀(1,…,1)= 0,и j (x) = 1, если f ₀(1,…,1) = 1. Для функции 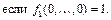С помощью f ₀и f ₁в [ N ]можно получить 0; 1 или` х. При наличии отрицания с помощью несамодвойственной функции 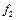в[ N ]можно построить константу, а следовательно, и вторую константу, т.е. можно построить 0 и 1. При наличии обеих констант с помощью немонотонной функции 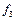можно построить отрицание. При наличии обеих констант и отрицания с помощью нелинейной функции f можно построить конъюнкцию. При наличии конъюнкции и отрицания с помощью законов де Моргана можно построить дизъюнкцию. Таким образом, в [ N ]построен полный класс {Ù, Ú, Ø} Þ [ N ]= Р ₂Þ N – полный класс. ■

Следствие. Из любой полной системы можно выделить полную подсистему, содержащую не более четырех функций.

Доказательство. Так как самодвойственная функция на противоположных наборах значений переменных принимает противоложные значения, то f ₀(1,…,1) = 1 означает, что f ₀ Ï S. Если же f ₀(0,…,0) = 1 Þ f ₀ Ï M. Отсюда вместо пяти разных функций в доказательстве достаточной теоремы можно брать только четыре, которые образуют полную систему. ■

Замечание. Число 4 в следствии не может быть понижено. Из следующей таблицы видно, что четыре функции по теореме Поста образуют полную систему, но после удаления любой из них система перестает быть полной:

	х ₁ х ₂	x ₁Å х₂Å х ₃
Т ₀
Т ₁
L
M
S

Упражнение

Полны ли системы булевых функций?

1) {Ø, Ù, Ú}; 2) {Ù, Ú}; 3) {Þ, Ù, Ú}; 4) {Ø};

5) {½}; 6) {¯}; 7) {Å, Ù, 1}; 8) {Þ, 0}.

4.8. Предполные классы

Класс булевых функций называется предполным, если он неполный, но при добавлении к нему любой функции, ему не принадлежащей, становится полным. Ясно, что предполный класс замкнут.

ТЕОРЕМА (Поста). Классы T ₀, T ₁, L, 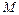, S предполные. Других предполных классов нет.

Доказательство. Если f ₀ Ï T ₀, то f ₀(x, …, x) = 1 или 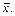В первом случае в [ T ₀ È { f ₀}]появляется полная система0, 1, Ù, Å,а во втором тоже полная системаÙ, Ø.Отсюда Т ₀ – предполный класс.

Если f ₁ Ï T ₁, то f ₁(x,…, x) = 0 или 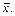В первом случае в [ T ₁ È { f ₁}]появляется полная система 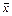= (х Þ 0), Ù, Ú, а во втором та же полная системаÙ, Ú, Ø.Отсюда Т ₁ – предполный класс.

Если f ₂ Ï S, то по лемме в [ S È { f ₂}]появляются0или1,а благодаря отрицанию, обе константы 0 и 1. С помощью h (x, y, z) = xy Ú xz Ú yz и константы 0 можно получить конъюнкцию h (x, y, 0)= ху. НаличиеÙ, Ø означает полноту множества [ S È { f ₂}].Отсюда, S – предполный класс.

Если f ₃ Ï M, то по лемме 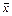Î [ M È { f ₃}].С учетом того, что Ù и Ú функции монотонные, получаем предполноту класса M.

Если f ₄ Ï L, то по лемме о нелинейной булевой функции можно построить конъюнкцию или отрицание конъюнкции. Так как 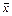Î L, то Ù, ØÎ [ L È { f ₄}] Þ L – предполный класс.

Пусть N – предполный класс, отличный от каждого из важнейших замкнутых классов. По теореме Поста о полноте системы такой класс полный. ■

4.9. Замкнутые классы

Из теоремы Поста следует, что любой замкнутый класс полностью принадлежит одному из важнейших замкнутых классов. Американский математик Эмиль Пост осуществил исследование структуры замкнутых классов в том же плане, в котором было изучено множество Р ₂.

Система функций из замкнутого класса N называется полной, если ее замыкание совпадает с этим классом N. Система функций из N называется базисом N, если она полна в N и независима. Например, можно показать, что система 0, 1, Ù, Ú – базис класса M. Приведем без доказательства теоремы:

ТЕОРЕМА. Замкнутый класс имеет конечный базис.

ТЕОРЕМА. Замкнутых классов в Р ₂ счетное число.

ГЛАВА 5. ГРАФЫ И СЕТИ

Графом называется пара множеств (V, X), где V – множество вершин, а X – некоторое множество неупорядоченных пар 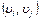элементов 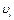и 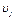из V, множество рёбер. Граф называется ориентированным (орграфом), если пары 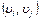упорядочены. В этом случае ребра называют дугами. Граф конечен, если множества V, X конечны. Ребро вида 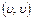называется петлёй. Рёбра 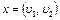и 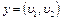называются кратными. Договоримся под словом граф подразумевать, если не оговорено противное, конечный граф без кратных рёбер и без петель. Если в графе существует ребро 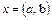, которое соединяет вершины а и b,то вершины а и b называют смежными, а вершину а и ребро x – инцидентными. Граф называется полным, если в нём любые две вершины смежны. Полный граф с р вершинами обозначается K_p. Например,