Изоморфизм графов. Пусть даны два графа Графы G1и G2называются изоморфными, если существуют взаимнооднозначные соответствия между множествами вершин и множествами рёбер этих

Пусть даны два графа 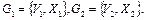Графы G ₁и G ₂называются изоморфными, если существуют взаимнооднозначные соответствия между множествами вершин и множествами рёбер этих графов, при этом соответствующие рёбра соединяют соответствующие вершины, т.е. если 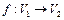, , 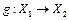то = .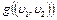

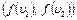Изоморфизм графов обозначаем G ₁ » G ₂. Множество всех графов разбивается на непересекающиеся классы изоморфности графов.

Пример. Все представители классов изоморфности орграфов с тремя вершинами и тремя рёбрами:

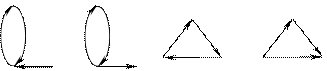
Рис. 5.3

Изоморфизм графа на себя называется автоморфизмом графа. Все автоморфизмы графа образуют группу относительно операции композиции отображений.

Дополнение 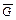графа G 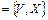имеет в качестве множества вершин множество V, а две вершины в 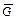смежны Û не смежны в G.

Пример.

G: :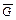

Рис. 5.4

Самодополнительный граф – это граф, который изоморфен своему дополнению. Наименьшие по числу рёбер нетривиальные самодополнительные графы.

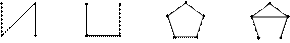
Рис. 5.5

Задача Рамсея. Доказать, что среди шести человек найдутся трое попарно знакомых или попарно незнакомых.

Решение. Шестивершинный граф либо его дополнения содержат треугольник.