Из любой несамодвойственной функции с помощью подстановки в нее вместо переменных тождественной функции и функции отрицания можно получить константу 0 или 1.
Доказательство. Пусть f Ï S Þ f ¹ f*. Это означает, что найдется набор значений переменных, для которого 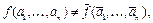 т.е.
т.е.
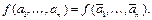 Если
Если 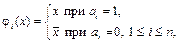
то 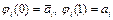 и для функции
и для функции 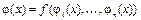 от одной переменной х имеем
от одной переменной х имеем 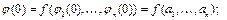
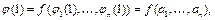 т.е.
т.е. 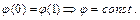 ■
■
ТЕОРЕМА (лемма о немонотонной булевой функции). Из любой немонотонной булевой функции с помощью подстановки в нее вместо переменных констант 0 и 1 и тождественной функции можно получить функцию отрицания.
Доказательство. Пусть f Ï M Þ $ a =< a 1, …, an >, b = < b 1,…, bn >, a µ b, но f (a) > f (b),т.е. f (a) =1, f (b) =0. Неравенство ai < bi, означает, что ai = 0, bi = 1.
Если 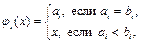
то 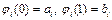 и для функции
и для функции 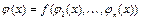 имеем
имеем 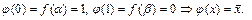 ■
■
ТЕОРЕМА (лемма о нелинейной булевой функции). Из любой нелинейной булевой функции с помощью подстановки в нее вместо переменных констант 0 и 1, тождественной функции, функции отрицания можно получить конъюнкцию или отрицание конъюнкции.
Доказательство. Представление нелинейной булевой функции f в виде полинома Жегалкина содержит слагаемое, в котором обязательно присутствуют конъюнкция каких-либо двух переменных. Изменение нумерации переменных не ослабит общности доказательства теоремы, и мы изменим нумерацию переменных таким образом, чтобы в полиноме Жегалкина присутствовало слагаемое с конъюнкцией х 1 х 2. Тогда, собрав в одну скобку все слагаемые, содержание х 1 х 2, в другую все слагаемые, содержание х 1,но не содержащие х 2,в третью – содержащие х 2, но не содержащие х 1, получим
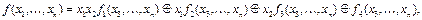 где в силу единственности представления булевой функции в виде полинома Жегалкина f 1
где в силу единственности представления булевой функции в виде полинома Жегалкина f 1 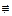 0, т.е. существует набор значений переменных, для которого
0, т.е. существует набор значений переменных, для которого 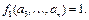
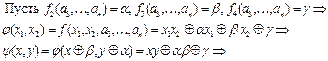
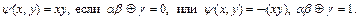 ■
■
 2015-06-28
2015-06-28 4309
4309
