Действия над машинами Тьюринга

Пусть машины 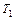и 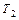имеют соответственно программы 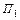и 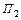и внутренние алфавиты этих машин не пересекаются. Пусть 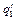– некоторое заключительное состояние машины 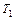, 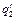– некоторое начальное состояние машины 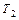. Заменим всюду в 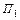состояние 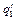на состояние 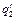и полученную программу объединим с программой 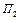. Новая программа П определяет машину Т =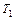 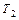, называемую композицией машин 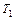и 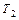по паре состояний (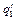, 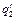). Внешний алфавит композиции является объединением внешних алфавитов машин 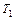и 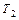. Эту же операцию можно применить к нескольким заключительным состояниям машины 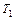для машин 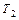, 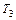. Тогда получим разветвление машин 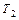и 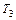, управляемое машиной .

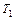Пусть 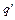– некоторое заключительное состояние машины Т, 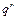– какое-либо состояние машины Т, не являющееся заключительным. Заменим всюду в программе П машины Т символ 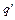на 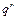. Получим программу 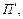определяющую итерацию машины Т по паре состояний 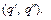Ее обозначение: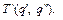

При задании сложных машин Тьюринга часто применяют операторную запись алгоритма по А.А. Ляпунову, которая представляет собой строку, состоящую из символов машин, символов перехода вида 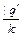и 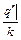, а также символов a и w, где a – символ начала работы, w – окончания работы. Например, 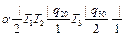w. Начинает работу машина 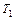. При достижении заключительного состояния 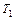включается в работу машина 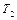. Если машина 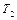достигнет состояния 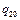, то работа оканчивается. При достижении машиной 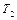другого заключительного состояния начинает работу машина 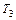. При достижении машиной 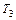заключительного состояния 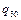начинает работу машина 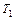, а при достижении машиной 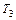другого заключительного состояния работа оканчивается.