Пусть в момент времени t самая левая непустая ячейка ленты содержит символ 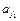 , а самая правая непустая ячейка содержит символ
, а самая правая непустая ячейка содержит символ 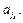 В этом случае будем говорить, что в момент t на ленте записано слово
В этом случае будем говорить, что в момент t на ленте записано слово 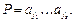 При S = 1, т.е. когда на ленте только один непустой символ Р =
При S = 1, т.е. когда на ленте только один непустой символ Р = 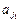 . Если в момент времени t автомат находится в состоянии
. Если в момент времени t автомат находится в состоянии 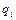 и в обозреваемой ячейке записан символ
и в обозреваемой ячейке записан символ 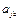 слова
слова 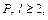 то слово
то слово 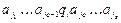 называется конфигурацией машины Тьюринга в момент t. Конфигурация, соответствующая началу работы машины, называется начальной. Результирующая конфигурация называется заключительной. Если в некоторый момент времени конфигурация машины была K, а в следующий момент
называется конфигурацией машины Тьюринга в момент t. Конфигурация, соответствующая началу работы машины, называется начальной. Результирующая конфигурация называется заключительной. Если в некоторый момент времени конфигурация машины была K, а в следующий момент 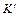 , то конфигурация
, то конфигурация 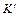 называется непосредственно выводимой из K и обозначается это так: K╞
называется непосредственно выводимой из K и обозначается это так: K╞ 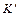 . Если
. Если 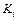 ╞
╞ 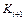 при
при 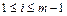 , то последовательность
, то последовательность 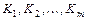 конфигураций называется вычислением по Тьюрингу. В этом случае пишем
конфигураций называется вычислением по Тьюрингу. В этом случае пишем 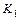 ├
├ 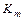 и говорим
и говорим 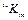 выводима из
выводима из 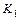 ”. Здесь
”. Здесь 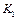 – начальная конфигурация. Если
– начальная конфигурация. Если 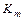 – заключительная конфигурация, то применяют запись
– заключительная конфигурация, то применяют запись 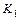 ├.
├. 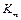 (читается:
(читается: 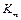 заключительно выводима из
заключительно выводима из 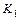 ). Если машина
). Если машина 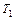 , начав работу на слове
, начав работу на слове 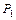 , остановится через определенное число шагов, то говорят, что машина Т применима к слову Р, а результат применения обозначается Т(Р). Если машина не остановится, то говорят, что машина Т не применима к слову Р. Машины
, остановится через определенное число шагов, то говорят, что машина Т применима к слову Р, а результат применения обозначается Т(Р). Если машина не остановится, то говорят, что машина Т не применима к слову Р. Машины 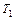 и
и 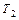 называются эквивалентными, если для любого Р слова
называются эквивалентными, если для любого Р слова 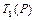 и
и 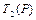 определены или не определены одновременно, и если они определены, то
определены или не определены одновременно, и если они определены, то 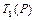 =
= 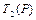 .
.
Язык конфигураций
|
|

Сейчас читают про:
 2015-06-28
2015-06-28 559
559







