Применяем к ДНФ 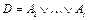 , реализующей булевы функции f, тождественные преобразования:
, реализующей булевы функции f, тождественные преобразования:
1) правило поглощения 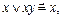 (1)
(1)
2) правило обобщенного склеивания 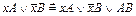 (2)
(2)
до тех пор, пока это можно. Получим некоторую ДНФ 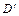 .
.
ТЕОРЕМА Квайна. ДНФ 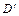 является сокращенной ДНФ булевой функции f.
является сокращенной ДНФ булевой функции f.
Доказательство. Рассмотрим любую простую для f конъюнкцию А, не входящую в 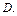 Докажем, что в процессе преобразований она будет введена в
Докажем, что в процессе преобразований она будет введена в 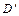 . Прежде всего заметим, что среди переменных А нет таких, которые не входят в
. Прежде всего заметим, что среди переменных А нет таких, которые не входят в 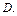 Допустим противное, что
Допустим противное, что 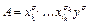 и переменная y не входит в
и переменная y не входит в 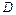 ,
, 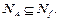 Множеству
Множеству 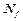 принадлежат все наборы, в которых
принадлежат все наборы, в которых 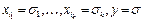 . Но
. Но 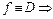 на таком наборе значений переменных
на таком наборе значений переменных 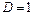
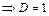 на любом наборе, на котором
на любом наборе, на котором 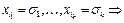 множеству
множеству 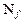 принадлежит любой набор, на котором конъюнкция
принадлежит любой набор, на котором конъюнкция 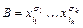 равна 1, т.е. имеем
равна 1, т.е. имеем 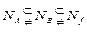 , а это означаeт, что ЭК А не простая для f.
, а это означаeт, что ЭК А не простая для f.
Рассмотрим все ЭК С, удовлетворяющие трем условиям:
1) С содержит только переменные, общие с 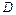 ;
;
2) 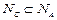 , т.е. А минимальна по рангу среди ЭК вида С;
, т.е. А минимальна по рангу среди ЭК вида С;
3) в ДНФ 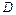 не существует ЭК Аj такой, что
не существует ЭК Аj такой, что 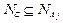 .
.
Множество ЭК С, удовлетворяющих условиям 1-3, непусто. Этим условиям удовлетворяет А. Обозначим одну из конъюнкция С наибольшего ранга через k. Эта конъюнкция не может включать все переменные 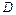 . В противном случае
. В противном случае 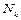 – точка в
– точка в 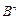 . Но всякая точка
. Но всякая точка 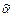 в этом пространстве содержится в
в этом пространстве содержится в 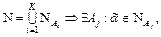 а это противоречит условию 3.
а это противоречит условию 3.
Пусть переменная 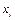 входит в
входит в 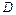 , но не входит в k. Рассмотрим конъюнкцию
, но не входит в k. Рассмотрим конъюнкцию 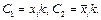 Их ранги больше ранга
Их ранги больше ранга 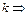 они не удовлетворяют условию 3. Это означает, что в
они не удовлетворяют условию 3. Это означает, что в 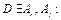
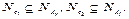
Конъюнкция 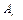 и
и 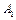 должны содержать
должны содержать 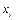 и
и 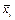 соответственно. В противном случае
соответственно. В противном случае 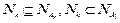 , что неверно для k в силу условия 3. Остальные сомножители
, что неверно для k в силу условия 3. Остальные сомножители 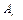 и
и 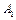 общие с
общие с 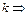 применяя к
применяя к 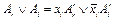 преобразование (2), введем в
преобразование (2), введем в 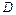 конъюнкцию
конъюнкцию 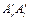 , которая либо в точности k, либо ее интервал содержит k.
, которая либо в точности k, либо ее интервал содержит k.
Аналогичные построения можно выполнить для любой конъюнкции наибольшего ранга, удовлетворяющей условиям 1-3. Тем самым доказано, что в процессе применения правила обобщенного склеивания к 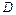 наибольший ранг конъюнкций С уменьшается по крайней мере на 1.
наибольший ранг конъюнкций С уменьшается по крайней мере на 1.
Повторяя рассуждения, заметим, что наступит момент, когда останется одна конъюнкция, удовлетворяющая условиям 1-3. Это А. Рассматривая ее вместо k, убеждаемся, что она будет введена в преобразованную ДНФ 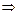 в преобразованную ДНФ войдут все простые ДНФ для f.
в преобразованную ДНФ войдут все простые ДНФ для f.
После включения ни одна такая конъюнкция не может быть удалена. Действительно, правило (2) ничего не удаляет из 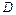 , а правило (1) удаляет только те ЭК, которые не являются простыми. Если в ДНФ будут введены все простые для f ЭК, то все остальные будут удалены по правилу поглощения.
, а правило (1) удаляет только те ЭК, которые не являются простыми. Если в ДНФ будут введены все простые для f ЭК, то все остальные будут удалены по правилу поглощения.
Пример. Если f = (01011110), то 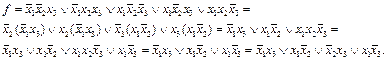
 2015-06-28
2015-06-28 2741
2741








