Сокращенная ДНФ

Интервал 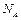называется максимальным для f, а ЭК А простой, если не существует допустимого интервала N_f такого, что 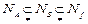. В приведенном примере максимальным являются 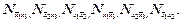Остальные допустимые интервалы (точки) содержатся в перечисленных. Например, 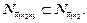Поэтому простыми конъюнкциями будут 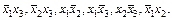Пусть 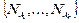– множество всех максимальных для f интервалов. Будем называть 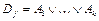сокращенной ДНФ (сокр. ДНФ). Сокр. ДНФ обладает замечательным свойством.

ТЕОРЕМА. Минимальная ДНФ для f получается из сокращенной удалением некоторых элементарных конъюнкций.

Лемма. 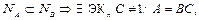где переменные C отличны от переменных В.

Доказательство леммы. Если переменные входят в А и В, то входят в одной и той же степени. Действительно, если это не так, то 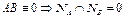, что противоречит условию 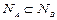. Пусть

Покажем, что множество 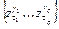пусто. Если оно не пусто, то рассмотрим набор 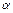такой, что

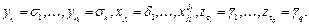
На этом наборе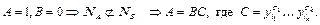

Следствие. Если 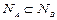, то ранг В меньше ранга А.

Доказательство теоремы. Пусть ЭК А, не являющаяся простой, вошла в мин. ДНФ f, т.е. мин. ДНФ 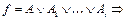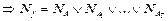и по лемме второму покрытию соответствует ДНФ меньшей сложности, что противоречит минимальности взятой ДНФ.