Для перехода от сокращенной ДНФ к тупиковой надо уметь проверять условие 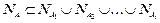 . (4)
. (4)
Не ограничивая общности, можно считать, что 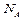 имеет непустое пересечение с
имеет непустое пересечение с 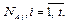 Действительно, если
Действительно, если 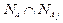 пусто, то от такого интервала
пусто, то от такого интервала 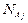 не зависит, выполнено ли условие (4). Если
не зависит, выполнено ли условие (4). Если 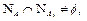 т.е.
т.е. 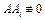 , то интервалы
, то интервалы 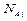 должны быть предварительно исключены из (4). Так как
должны быть предварительно исключены из (4). Так как 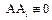 , то общие для
, то общие для  и
и 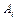 переменные входят в них в одинаковых степенях. Удалим из всех
переменные входят в них в одинаковых степенях. Удалим из всех 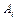 переменные, общие с
переменные, общие с  . Например, если
. Например, если 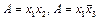 , то удалим из
, то удалим из 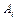 переменную
переменную 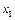 . Оставшиеся в
. Оставшиеся в 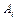 сомножители образуют конъюнкцию С. Если все сомножители
сомножители образуют конъюнкцию С. Если все сомножители 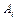 входят в
входят в  , то полагаем
, то полагаем 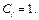
ТЕОРЕМА (критерий поглощения) 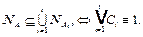
Доказательство. 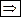
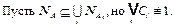 Следовательно, существует набор
Следовательно, существует набор 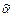 значений переменных такой, что
значений переменных такой, что 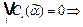
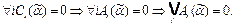
Если 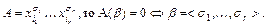
Переменные из  не входят в
не входят в 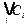 . Рассмотрим набор, составленный из
. Рассмотрим набор, составленный из 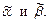 Обозначим такой объединенный набор через
Обозначим такой объединенный набор через 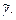
Тогда 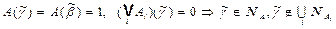 . Противоречие.
. Противоречие.
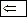
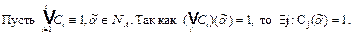
 Но тогда
Но тогда 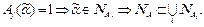
Для получения тупиковой ДНФ из сокращенной необходимо последовательно применять доказанный критерий поглощения. Те конъюнкции, для которых не выполнено условие 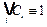 , включаем в состав тупиковой ДНФ.
, включаем в состав тупиковой ДНФ.
Пример. Рассмотрим булеву функцию, заданную в виде сокр. ДНФ (см. предыдущий пример), 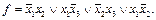 Проверяем конъюнкцию
Проверяем конъюнкцию 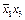 . Так как
. Так как 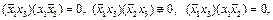 то необходимо проверить условие
то необходимо проверить условие 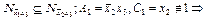 в ДНФ следует поставить
в ДНФ следует поставить 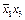 . Аналогичный результат дает проверка
. Аналогичный результат дает проверка 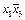 . Для испытания
. Для испытания 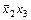 остается две конъюнкции
остается две конъюнкции 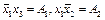 . Мы имеем
. Мы имеем 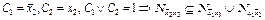 . Удалив
. Удалив 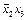 , придем к тупиковой ДНФ
, придем к тупиковой ДНФ 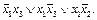 Проведя испытания в другом порядке, можно получить и другую тупиковую ДНФ
Проведя испытания в другом порядке, можно получить и другую тупиковую ДНФ 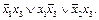
Замечание. Минимальная ДНФ – тупиковая. Но не наоборот. Для построения мин. ДНФ необходим перебор всех тупиковых ДНФ данной функции.
 2015-06-28
2015-06-28 1084
1084








