ОТЧЕТ К ЛАБОРАТОРНОЙ РАБОТЕ
Название работы:
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ В ПАРАЛЛЕЛЬНОМ LC-КОНТУРЕ
| Факультет_______________________ | Работа №__________________________ |
| Группа__________________________ | Дата выполнения___________________ |
| ФИО преподавателя___________________ | ФИО студента______________________ |
Подпись исполнителя ___________________
Работу принял “ _____ ” ____________ 200 г. ___________________________________
Подпись и ФИО преподавателя
1. Цель работы: исследование параллельного LC-контура в режиме вынужденных колебаний; измерение и вычисление резонансной частоты, полосы пропускания, добротности.
2. Оборудование: лабораторная установка, генератор сигналов синусоидальной и прямоугольной формы, осциллограф, соединительные провода.
3. Краткая теория: При наличии в цепи колебательного контура внешних ЭДС в контуре возникают вынужденные колебания, имеющие частоту внешнего источника. Чтобы вызвать вынужденные колебания, к контуру необходимо приложить внешнее периодически изменяющееся напряжение или пропустить через него периодически изменяющийся ток. При приближении частоты внешнего электрического воздействия к некоторому значению, характерному для данного контура, амплитуда тока резко возрастает. Частоту, при которой осциллирующая величина достигает максимального значения, называется резонансной. Зависимость амплитуды осциллирующей величины (напряжение, сила тока и т.д.) от частоты внешнего вынуждающего воздействия называется амплитудно-частотной характеристикой (АЧХ).
Для характеристики колебательной системы часто используется величина добротности (Q). В частности, добротность характеризует остроту резонансных кривых. Рассмотрим ширину кривой Dn (рис.1), взятую на высоте 0,7. Величину Dn=n2-n1 называют полосой пропускания контура. Относительная ширина полосы пропускания контура оказывается обратно пропорциональной величине его добротности:
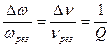 (1)
(1)
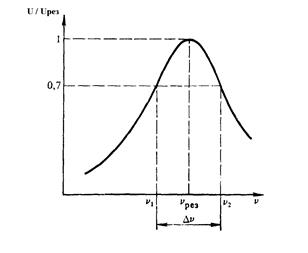
Рис.1. Определение полосы пропускания контура.
Уравнение затухающих колебаний для LC-контура имеет вид
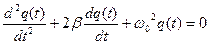 (2)
(2)
где q(t) – заряд на конденсаторе, b=r/(2L) – коэффициент затухания, w0=1/(LC)1/2 – собственная частота.
Для LC–контура добротность
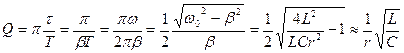 (3)
(3)
Так как для конденсатора q=CUc, (Uc – напряжение на конденсаторе), то для зависимости амплитуды напряжения от времени получаем аналогичное выражение:
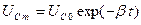 .
.
| υ (Гц) | U (В) |
| 0,06 | |
| 0,07 | |
| 0,08 | |
| 0,08 | |
| 0,09 | |
| 0,10 | |
| 0,11 | |
| 0,11 | |
| 0,10 | |
| 0,105 | |
| 0,115 | |
| 0,120 | |
| 0,130 | |
| 0,135 | |
| 0,145 |
| 0,160 | |
| 0,165 | |
| 0,19 | |
| 0,21 | |
| 0,22 | |
| 0,25 | |
| 0,27 | |
| 0,29 | |
| 0,32 | |
| 0,34 | |
| 0,4 | |
| 0,42 | |
| 0,46 | |
| 0,5 | |
| 0,54 | |
| 0,6 |
| 0,68 | |
| 0,75 | |
| 0,85 | |
| 0,95 | |
| 1,05 | |
| 1,25 | |
| 1,45 | |
| 3600 | 1,55 |
| 1,4 | |
| 1,25 | |
| 1,15 | |
| 0,9 | |
| 0,8 | |
| 0,75 |
5. Обработка экспериментальных данных:
1. Δυ = 5000-2700= 2300
2. 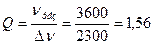
1. T = 0.9 мS
2. τ =
3. 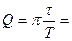
6. Вывод:
 2015-06-28
2015-06-28 1076
1076






