Амплитуда и фаза вынужденных колебаний

Рассмотрим, зависит ли амплитуда вынужденных колебаний А от частоты w и как. Механические и электромагнитные колебания будем рассматривать одновременно.

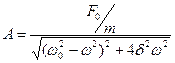	,	(9.1)
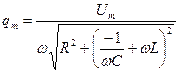	.	(9.2)

Найдем максимум формул (9.1), (9.2), т.е. реальную частоту, при которой амплитуда смещения или заряда достигает максимума.

Продифференцируем подкоренное выражение (9.1) и (9.2) по w и приравняем эти выражения к 0. Получаем:

.

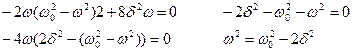(9.3)

Равенство (9.3) выполняется при:

w = 0

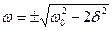– физический смысл имеет значение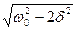

Резонансная частота равна:

.

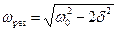(9.4)

Резонансом механическим или электрическим называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к резонансной частоте.

Если d² << w², то w_рез@ w_о, тогда подставим (9.4) в (9.1).

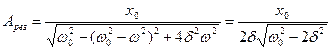
Чем меньше d, тем правее лежит максимум данной кривой.

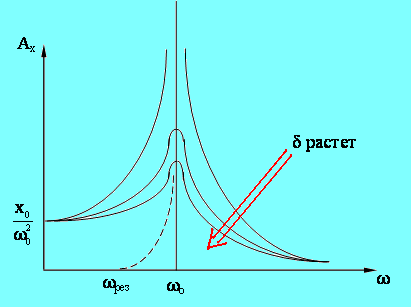
Графически зависимость А = f (w) при различных значениях d можно представить в виде графика:

а)

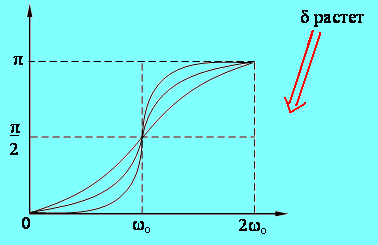
б)

Рис. 9.1. Графики зависимостей амплитуды и фазы колебаний как функции от циклической частоты ω.

Если d = 0, то j = 0 (фазы одинаковы)

Если w ® 0, то все кривые приходят к одному и тому же предельному значению:

.

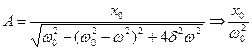(9.5)

эта величина называется статическим отклонением.

А совокупность кривых – резонансными кривыми.

Для механических колебаний:

.

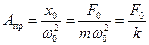(9.6)

Для электромагнитных колебаний:

.

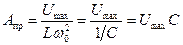(9.7)

Если же w ® ¥, то все кривые асимптотически стремятся к 0.

Если затухание мало (d₂ << w²_о), то

А_рез = x_ow_о² / 2dLw_о = 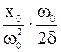=x_oQ/w_о²

Для мех.

А_рез=F_oQ/mw_о²

Q_мех=w_о² / 2d A_рез=U_oQLC/L

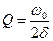(9.8)

добротность колебательного контура.

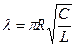	,	(9.9)
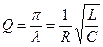	.	(9.10)

Добротность (колебательной системы) характеризует свойства колебательной системы, чем больше добротность, тем больше резонансная амплитуда.