Свойства систем векторов линейного пространства

Теорема 1. Если система векторов содержит нулевой вектор, то она линейно зависима.

Док-во. Пусть, например, 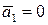. Тогда равенство 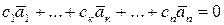справедливо при с₁=1, с₂=с₃=…=с_п= 0, т.е. при ненулевом коэффициенте с₁. Значит, система линейно зависима.

Теорема 2. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.

Док-во. Пусть, например, векторы 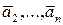линейно зависимы. Тогда в равенстве 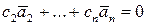не все коэффициенты равны нулю. Но тогда при тех же коэффициентах и с₁ =0 будет справедливо и равенство 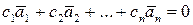. Система линейно зависима.

Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.

Доказывается «от противного».

Теорема 3 (теорема Штейница). Если каждый из векторов 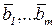является линейной комбинацией векторов 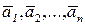и m>n, то система векторов 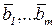линейно зависима.

Следствие. В любой системе п -мерных векторов не может быть более чем п линейно независимых.

Док-во. Каждый п -мерный вектор выражается в виде линейной комбинации п единичных векторов. Поэтому, если система содержит т векторов и т > п, то по теореме Штейница эта система линейно зависима.

Линейное пространство называется п -мерным, если в нем существуют п линейно независимых векторов, а любые п+1 векторов являются линейно зависимыми.