Задание 1. Абитуриент считается зачисленным в вуз, если сумма полученных им на экзаменах оценок не меньше проходного балла и оценка по математике выше тройки. Найти количество абитуриентов, поступивших в вуз.
| A | B | C | D | E | F | |
| Проходной | балл: | |||||
| Фамилия | Математика | Русский язык | Литература | Сумма | Зачислен | |
| Антонов | ||||||
| Воробьев | ||||||
| Синичкин | ||||||
| Воронина | ||||||
| Снегирев | ||||||
| Соколова | ||||||
| Поступили: |
Замечание. При нахождении количества поступивших в вуз абитуриентов воспользуйтесь логической функцией СЧЕТЕСЛИ. Информацию о ней найдите самостоятельно в справочной системе.
Задание 2. Пять абонентов звонят из города А в город Б. Если телефонный междугородный звонок был произведен в выходные дни (суббота, воскресенье), или в праздничные дни, или в будние дни с 20 часов вечера до 8 часов утра, то он рассчитывается по льготному тарифу со скидкой 50%, во все оставшееся время льготы нет. Подсчитать, сколько каждый из пяти абонентов должен заплатить за переговоры.
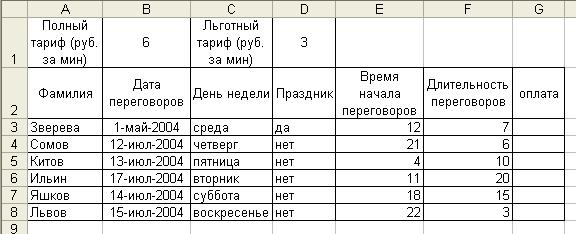
Замечание. Если звонок идет по льготному тарифу, то должно выполняться условие: День недели = "суббота" ИЛИ День недели = "воскресенье" ИЛИ Праздник = "да" ИЛИ Время начала переговоров >= 20 ИЛИ Время начала переговоров <= 8.
Поэтому в ячейку G3 заносим формулу:
ЕСЛИ(ИЛИ (С3="суббота"; С3="воскресенье"; ВЗ="Да"; Е3>=20; Е3<=8); $D$1*F3; $B$1*F3). Ссылки на ячейки D1 и В1 абсолютные, так как при копировании формул имена этих ячеек не должны меняться.
Задание 3. Олимпиада по программированию оценивается по сумме очков, полученных за каждую из трех задач, плюс 0,1 от набранной суммы для учащихся классов младше 10-го. В олимпиаде принимало участие 12 человек: 4 из 8-го класса, 3 – из 9-го, 3 – из 10-го и 2 – из 11-го. Первое задание оценивалось максимум в 10 баллов. Второе – в 8, третье – в 12. Набравшие больше 27 баллов получают диплом 1-й степени, больше 25 – 2-й степени, больше 23 – третьей степени. Создайте таблицу участников и их результатов. Определите дипломы участников. Постройте диаграмму по сумме набранных очков для получивших диплом 1-й, 2-ой и 3-ей степеней.
Задание 4. Компания по снабжению электроэнергией взимает плату с клиентов по тарифу: 0,6 рубля за 1 кВт/ч за первые 200 кВт/ч; 0,9 рубля за 1 кВт/ч, если потребление свыше 200 кВт/ч, но не превышает 500 кВт/ч; 1,2 рубля за 1 кВт/ч, если потребление свыше 500 кВт/ч. Услугами компании пользуются 10 клиентов. Подсчитать плату для каждого клиента. Определить, сколько клиентов потребляют свыше 500 кВт/ч.
Задание 5. Провести статистическую обработку данных: Составить вариационный ряд, построить гистограмму частот, полигон относительных частот. Найти размах варьирования, х ср, D(x) - дисперсию, σ(x) - среднее квадратичное отклонение, V - коэффициент вариации, моду, медиану.
Вариант 1. Дана исходная таблица распределения 30 абитуриентов по числу баллов, полученных ими на вступительных экзаменах.
| Баллы | |||||||||
| Число студентов |
Вариант 2. В эксперименте по заучиванию ряда из 10 двузначных чисел результаты заучивания после первого предъявления составили для 35 испытуемых следующие величины: 5, 3, 5, 5, 4, 3, 4, 3, 1, 4, 5, 4, 4, 3, 4, 5, 3, 3, 4, 5, 4, 2, 3, 2, 2, 4, 3, 4, 3, 3, 4, 2, 4, 5.
Вариант 3. Среди 38 учеников в начале учебного года проводилась контрольная работа по чтению (максимальное количество очков – 128). Получены следующие результаты: 90, 66, 106, 84, 105, 83, 104, 82, 97, 97, 59, 95, 78, 70, 47, 95, 100, 69, 44, 80, 75, 75, 51, 109, 89, 58, 59, 72, 74, 75, 81, 71, 68, 112, 62, 91, 93, 84.
Вариант 4. Преподаватель предложил 125 учащимся контрольное задание, состоящее из 40 вопросов. В качестве оценки теста выбиралось количество вопросов, на которые были получены правильные ответы. Дискретное распределение частот приведено в таблице.
| Оценка | ||||||||||||||
| Частота |
Вариант 5. Имеются результаты (в см), показанные группой школьников (70 чел) в тесте «Прыжок в высоту с места» 35, 39, 30, 30, 27, 25, 45, 24, 30, 47, 28, 31, 41, 36, 38, 40, 25, 31, 41, 25, 31, 39, 31, 36, 38, 36, 27, 29, 30, 31, 35, 31, 35, 41, 36, 40, 36, 31, 40, 36, 51, 36, 38, 33, 29, 32, 35, 40, 42, 44, 44, 42, 44, 42, 44, 42, 37, 30, 30, 28, 36, 37, 45, 32, 41, 32, 31, 30, 29, 26.
Вариант 6. 30 учеников 10 класса Новоторъяльской средней школы республики Марий Эл при проведении теста сгибание и разгибание рук в упоре показали следующие результаты (кол. раз): 39, 68, 34, 35, 38, 37, 34, 36, 35, 20, 18, 17, 20, 19, 16, 16, 17, 17, 17, 17, 16, 40, 25, 26, 30, 34.
Вариант 7. 20 учеников 9 класса одной из школ Кировской области при проведении теста бег на 1000 м показали следующие результаты (мин. сек): 3,53; 3,55; 3,55; 3,54; 3,50; 3,51; 3,50; 4,39; 4,40; 4,38; 4,42; 4,35; 4,41; 4,37; 4,38; 4,43; 4,46; 4,39; 4,40.
Задание 6. Определить имеются ли существенные различия между средними значениями двух выборок.
Вариант 1. Изучался уровень абстрактного мышления в двух 3-их классах одной параллели у учеников одной школы. Был разработан соответствующий тест и предложен ученикам: 20 учеников 3-А показали следующие результаты (Х): 19, 32, 33, 44, 38, 35, 39, 39, 44, 44, 24, 37, 29, 40, 42, 32, 48, 43, 33, 47, а 15 учеников 3-Б следующие результаты (Y): 17, 7, 17, 28, 27, 31, 20, 17, 35, 43, 10, 28, 13, 43, 45.
Вариант 2. В опытах Небылицина В.Д. испытуемые по одному из показателей (по скорости угасания условного рефлекса) образовали 2 группы: лица с преобладанием возбуждения и лица уравновешенные. С этими же испытуемыми были проведены опыты по определению a-индекса. Для группы возбудимых (7 человек) получены следущие значения a-индекса: 91, 56, 73, 51, 82, 46, 78. Для группы уравновешенных (15 человек): 65, 72, 82, 95, 78, 84, 88, 81, 94, 70, 68, 83, 96, 92, 89.
Вариант 3. Изучалось представление школьников о различных временных интервалах, в т.ч. и представления о минутном интервале. Испытуемые нажимали кнопку секундомера, пускали его в ход, и когда, по их мнению, проходила минута, останавливали его. Смотреть на циферблат испытуемые не могли. Показания секундомера у 20 учеников III класса составили следующий ряд (в сек.): 2,4; 3,9; 4,7; 9,1; 11,0; 12,7; 14,9; 16,0; 20,8; 25,3; 29,0; 30,6; 32,1; 32,7; 33,3; 36,3; 38,1; 43,5; 47,4; 53,8, а у 20 учеников V класса: 2,9; 12,5; 13,0; 13,5; 17,2; 17,7; 20,5; 22,7; 24,6; 26,3; 29,7; 30,7; 31,8; 33,8; 38,5; 42,8; 53,8; 55,9; 60,6; 76,1. Имеется ли существенное различие между представлениями о минутном интервале у учеников III и V классов?
Задание 7. С помощью статистических методов изучить зависимость между величинами.
Вариант 1. Приводятся данные о продолжительности ознакомления (в сек.) и времени воспроизведения (в сек.) системы пространственных линий.
Ознакомление: 2,5; 1,9; 3,7; 2,0; 4,3; 2,4; 2,3; 4,8; 1,7; 3,2; 3,6; 2,3; 4,9; 1,8; 2,8; 4,0; 1,8; 3,0; 2,4; 4,5; 2.3; 3,4; 2,0; 2,5.
Восприятие: 3,2; 1,5; 2,4; 3,6; 4,5; 3,0; 3,1; 4,2; 2,9; 3,5; 4,0; 3,0; 4,3; 2,5; 2,9; 3,6; 2,5; 3,2; 2,9; 3,9; 2,7; 3,6; 2,4; 3,0.
Вариант 2. 25 учеников 9 класса одной из школ города Йошкар-Олы при проведении теста удержание тела в висе на перекладине показали следующие результаты (сек): 37, 69, 27, 46, 50, 46, 46, 45, 40, 35, 35, 35, 36, 35, 36, 35, 35, 35, 35, 35, 35, 37, 38, 39, 45, а при проведении теста сгибание и разгибание рук в упоре (кол. раз): 39, 68, 34, 35, 38, 37, 34, 36, 35, 20, 18, 17, 20, 19, 16, 16, 17, 17, 17, 17, 16, 50, 41, 34, 35. Оценить тесноту взаимосвязи между этими двумя тестами, построить график зависимости.
Вариант 3. Можно ли утверждать, что мнения двух судей, оценивавших на соревнованиях по фигурному катанию выступления мужчин в обязательных упражнениях, были согласованными, если они поставили 9 участникам следующие оценки:
Судья 1: 4.7, 4.9, 5.1, 5.6, 5.7, 5.3, 5.8, 5.9, 5.5
Судья 2: 4.3, 4.5, 5.3, 5.2, 5.5, 5.5, 5.9, 5.6, 5.7
Вариант 4. Представлены данные, полученные на соревнованиях на дистанции 15 км для двух групп лыжников: первые проходили дистанцию традиционными ходами, а вторые - коньковым. Сравнить числовые характеристики этих двух групп (если данные несгруппированы).
1 гр.: 37,02; 36,74; 37,82; 38,12; 36,91; 37,28; 38,21; 37,51; 37,56; 38,25
2 гр.: 35,81; 35,61; 35,02; 35,53; 35,84; 35,12; 26,12; 36,49; 35,62; 36,28.
 2015-06-28
2015-06-28 7719
7719
