а) 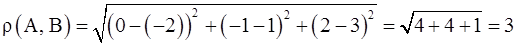 ;
;
б) угол В в треугольнике АВС есть угол между векторами 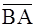 и
и 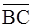 . Имеем
. Имеем 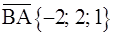 ,
, 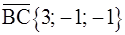 ,
, 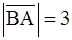 ,
, 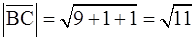 ,
,
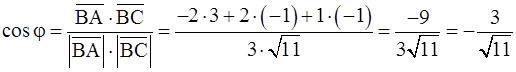 ;
;
в) 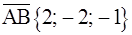 ,
, 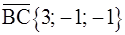 ,
, 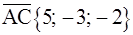 ,
,
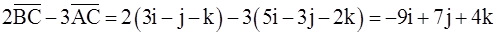 ,
,
отсюда находим
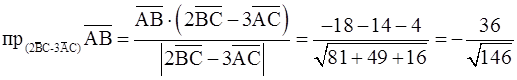 ;
;
г) 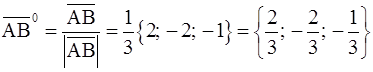 .
.
Направляющими косинусами вектора 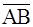 являются 2/3, –2/3, –1/3.
являются 2/3, –2/3, –1/3.
Векторным произведением 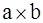 упорядоченной пары неколлинеарных векторов а и b называется вектор c, удовлетворяющий следующим трём требованиям:
упорядоченной пары неколлинеарных векторов а и b называется вектор c, удовлетворяющий следующим трём требованиям:
1) 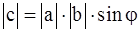 , где j – угол между векторами а и b;
, где j – угол между векторами а и b;
2) с перпендикулярен каждому из векторов а и b;
3) а, b, с образуют правую тройку.
Векторное произведение принято также обозначать 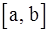 .
.
Теорема 5. a) 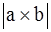 равен площади параллелограмма, построенного на векторах а и b; б) а ´ b = – b ´ a; в) а ´ (b + c) = а ´ b + + а ´ c; г) (l а) ´ b = l(а ´ b).
равен площади параллелограмма, построенного на векторах а и b; б) а ´ b = – b ´ a; в) а ´ (b + c) = а ´ b + + а ´ c; г) (l а) ´ b = l(а ´ b).
Теорема 6. Если 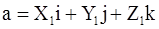 ,
, 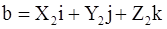 , то
, то 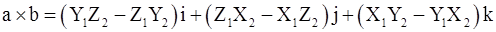 ,
,
или, в символической записи,
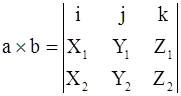 .
.
Смешанным произведением упорядоченной тройки векторов а, b, с называется число (a ´ b) с; смешанное произведение векторов а, b, с обозначается(а, b, с).
Теорема 7. а) а, b, с компланарны в том и только в том случае, если (а, b, с) = 0;
б) для некомпланарной тройки векторов а, b, с (а, b, с) > 0 в том и только в том случае, если а, b, с образуют правую тройку, и (а, b, с) < 0 в том и только в том случае, если а, b, с образуют левую тройку;
в) |(а, b, с)| равен объёму параллелепипеда, построенного на векторах а, b, с;
г) (а, b, с) = (b, c, a) = (c, a, b) = –(b, a, с) = –(а, c, b) = –(c, b, a).
Теорема 8. Если 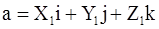 ,
, 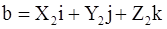 ,
, 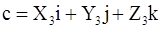 , то
, то
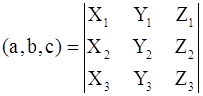 .
.
Пример 3. Даны точки A(4;–1;3), B(0;1;2), C(3;–2;5), D(1;–1;1). Найти: а) площадь треугольника АВС; б) высоту 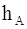 треугольника АВС, опущенную из вершины А на сторону ВС;
треугольника АВС, опущенную из вершины А на сторону ВС;
в) объём пирамиды АВСD.
Решение. а) Площадь 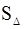 треугольника АВС равна половине площади параллелограмма S, построенного на векторах
треугольника АВС равна половине площади параллелограмма S, построенного на векторах 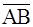 и
и 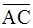 , т.е.
, т.е. 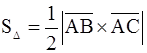 . Имеем
. Имеем 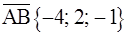 ,
, 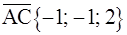 ,
,
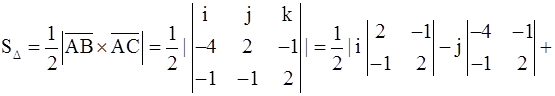
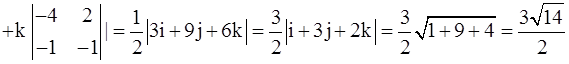 ;
;
б) 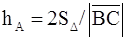 ;
; 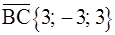 ,
, 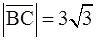 ;
; 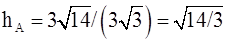 .
.
в) Объём 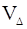 пирамиды АВСD равен
пирамиды АВСD равен 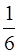 объёма параллелепипеда, построенного на векторах
объёма параллелепипеда, построенного на векторах 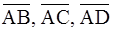 . Имеем
. Имеем 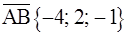 ,
, 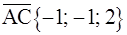 ,
, 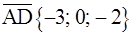 ;
;
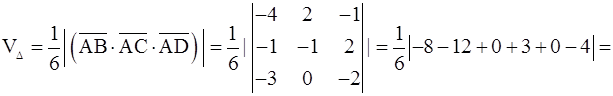
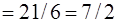 .
.
2. Прямая на плоскости
Прямая на плоскости, в которой определена прямоугольная система координат, может быть задана следующими уравнениями:
Ax + By + C = 0 – общее уравнение;
y = kx + b – уравнение с угловым коэффициентом (k – угловой коэффициент – есть тангенс угла наклона прямой к оси 0x);
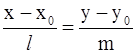 – каноническое уравнение (прямая проходит через точку M(x0; y0) параллельно вектору
– каноническое уравнение (прямая проходит через точку M(x0; y0) параллельно вектору 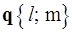 – направляющему вектору прямой);
– направляющему вектору прямой);
A(x – x0) + B(y – y0) = 0 – уравнение прямой, проходящей через точку M(x0; y0) перпендикулярно вектору 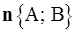 – нормали прямой;
– нормали прямой;
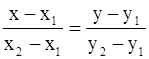 – уравнение прямой, проходящей через точки
– уравнение прямой, проходящей через точки
M1(x1; y1), M2(x2; y2).
Уравнение прямой, параллельной оси Oy и проходящей через точку
(a; 0), имеет вид x = a.
Пример 4. Составить уравнения прямых: а) AB; б) BC; в) CD.
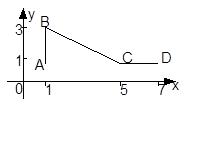 Решение. а) АВ параллельна 0y, поэтому её уравнением будет x = 1.
Решение. а) АВ параллельна 0y, поэтому её уравнением будет x = 1.
б) составим уравнение ВС как прямой, проходящей через точки B(1; 3), C(5; 1):
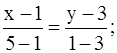
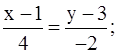
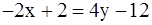 ;
; 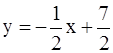 .
.
в) Прямая СD параллельна 0x, поэтому уравнением СD является y = 1.
3. Полярная система координат
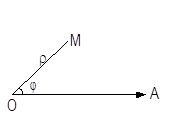 Полярная система координат определяется заданием точки 0, называемой полюсом, исходящего из этой точки луча 0А, называемого полярной осью, и масштаба для измерения длины.
Полярная система координат определяется заданием точки 0, называемой полюсом, исходящего из этой точки луча 0А, называемого полярной осью, и масштаба для измерения длины.
Каждой точке М на плоскости ставятся в соответствие два числа: 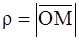 – полярный радиус и j – полярный угол, на который нужно повернуть полярную ось для совмещения с вектором
– полярный радиус и j – полярный угол, на который нужно повернуть полярную ось для совмещения с вектором 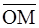 ; при этом вращение против часовой стрелки считается положительным, по часовой стрелке – отрицательным. Если точка М совпадает с полюсом 0, то полярный угол не определён.
; при этом вращение против часовой стрелки считается положительным, по часовой стрелке – отрицательным. Если точка М совпадает с полюсом 0, то полярный угол не определён.
Полярный угол j определяется с точностью до 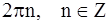 . Принято договариваться о главных значениях полярного угла; обычно таковыми считаются углы в пределах
. Принято договариваться о главных значениях полярного угла; обычно таковыми считаются углы в пределах 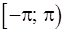 или
или 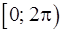 .
.
Рассмотрим декартову прямоугольную систему координат на плоскости, начало которой совпадает с полюсом 0, а положительная
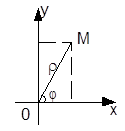 полуось 0x – с полярной осью (в этом случае говорят, что декартова прямоугольная система координат согласована с полярной системой координат). Тогда декартовы прямоугольные (x; y) и полярные (r; j) координаты точки М связаны соотношениями
полуось 0x – с полярной осью (в этом случае говорят, что декартова прямоугольная система координат согласована с полярной системой координат). Тогда декартовы прямоугольные (x; y) и полярные (r; j) координаты точки М связаны соотношениями
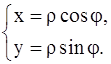
Это есть формулы перехода от полярных координат к декартовым.
Пример 5. Найти полярные координаты точки М, если в согласованной декартовой прямоугольной системе координат она имеет координаты 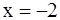 ,
, 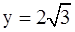 .
.
Решение. 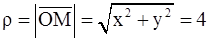 ;
;
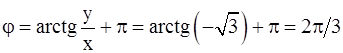 .
.
Пример 6. Составить полярные уравнения:
а) прямой 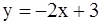 ; б) параболы y = 2x2.
; б) параболы y = 2x2.
Решение. Имеем x = r cosj, y = r sinj. Поэтому
а) 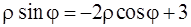 ;
; 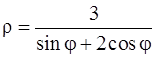 – уравнения прямой
– уравнения прямой
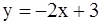 .
.
б) r sinj = 2 r2 cos2j, 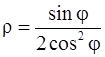 – уравнения параболы y = 2x2.
– уравнения параболы y = 2x2.
4. Плоскость и прямая в пространстве
Плоскость (P) в пространстве с заданной декартовой прямоугольной системой координат может быть задана одним из следующих уравнений:
1) Ax + By + Cz + D = 0 – общее уравнение плоскости;
2) A(x – x0) + B(y – y0) + C(z – z0) = 0 – уравнение плоскости (P), проходящей через точку M(x0; y0; z0) и перпендикулярной вектору 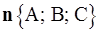 – вектору нормали к (P) (вектором нормали к плоскости (P) называется любой ненулевой вектор, перпендикулярный (P));
– вектору нормали к (P) (вектором нормали к плоскости (P) называется любой ненулевой вектор, перпендикулярный (P));
3) 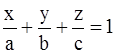 – уравнение плоскости в отрезках, где a, b, c –направленные отрезки, отсекаемые плоскостью на осях 0x, 0y, и 0z соответственно;
– уравнение плоскости в отрезках, где a, b, c –направленные отрезки, отсекаемые плоскостью на осях 0x, 0y, и 0z соответственно;
4) 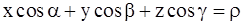 – нормированное (или нормальное) уравнение плоскости (P), где cosa, cosb, cosg – направляющие косинусы вектора нормали n к (P), направленного из начала координат в сторону плоскости (P), r – расстояние от начала координат до плоскости (P);
– нормированное (или нормальное) уравнение плоскости (P), где cosa, cosb, cosg – направляющие косинусы вектора нормали n к (P), направленного из начала координат в сторону плоскости (P), r – расстояние от начала координат до плоскости (P);
5) 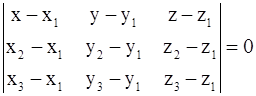 – уравнение плоскости,
– уравнение плоскости,
проходящей через три точки M1(x1; y1; z1), M2(x2; y2; z2), M3(x3; y3; z3), не лежащие на одной прямой.
Расстояние от точки M0(x0; y0; z0) до плоскости (P), заданной общим уравнением Ax + By + Cz + D = 0, находится по формуле
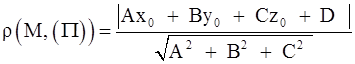 .
.
Две различные плоскости (P1): 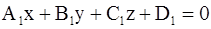 и (P2):
и (P2): 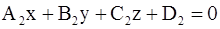 параллельны в том и только в том случае, если
параллельны в том и только в том случае, если 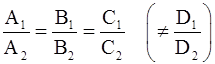 .
.
Угол j между плоскостями (P1): 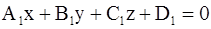 и (P2):
и (P2): 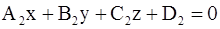 есть угол между нормалями
есть угол между нормалями 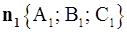 и
и 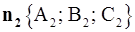 (с поправкой на направление, если угол тупой) к этим плоскостям:
(с поправкой на направление, если угол тупой) к этим плоскостям:
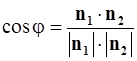 .
.
Эти плоскости: а) параллельны в том и только в том случае, если 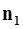 и
и 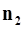 коллинеарны; б) перпендикулярны в том и только в том случае, если
коллинеарны; б) перпендикулярны в том и только в том случае, если 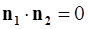 .
.
Прямая (L) в пространстве с заданной прямоугольной системой координат может быть задана:
1) каноническими уравнениями 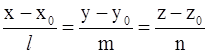 ; при этом (L) проходит через точку M0(x0; y0; z0) и параллельна направляющему вектору прямой
; при этом (L) проходит через точку M0(x0; y0; z0) и параллельна направляющему вектору прямой 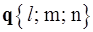 ;
;
2) параметрическими уравнениями
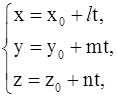
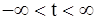 ,
,
заданные числа x0, y0, z0, l, m, n имеют тот же смысл, что и в канонических уравнениях;
3) общим уравнением
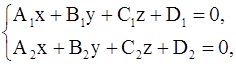
где ранг матрицы 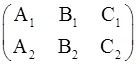 равен 2, при этом (L) есть прямая пересечения плоскостей
равен 2, при этом (L) есть прямая пересечения плоскостей
(P1): 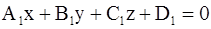 , (P2):
, (P2): 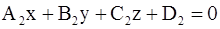 .
.
Угол j между прямыми (L1) и (L2) есть угол между направляющими векторами 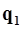 и
и 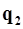 (с поправкой на направление, если угол между ними тупой):
(с поправкой на направление, если угол между ними тупой):
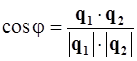 .
.
Угол y между прямой (L): 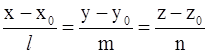 и плоскостью (P):
и плоскостью (P): 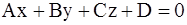 определяется по формуле
определяется по формуле
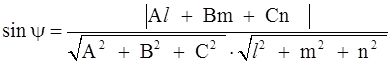 .
.
Пример 7. Даны плоскость (P): 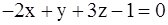 , прямая (L):
, прямая (L): 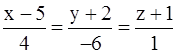 и точка M(–4; 1; 7): а) составить уравнение плоскости, проходящей через точку М и параллельной (P); б) составить канонические уравнения прямой, проходящей через точку М и параллельной (L); в) составить уравнение плоскости, проходящей через
и точка M(–4; 1; 7): а) составить уравнение плоскости, проходящей через точку М и параллельной (P); б) составить канонические уравнения прямой, проходящей через точку М и параллельной (L); в) составить уравнение плоскости, проходящей через
точку М и перпендикулярной (L); г) составить уравнение прямой, проходящей через точку М и перпендикулярной (P¢);
д) составить уравнение плоскости, проходящей через точку М и прямую(L); е) составить уравнение плоскости, проходящей через точку М и перпендикулярной плоскостям (P¢): x – 3y – z + 2 = 0 и
(P¢¢): 4x + 2y – 5z + 7 = 0; ж) найти точку пересечения прямой (L) и плоскости (P); з) найти расстояние от точки М до плоскости (P).
Решение. а) В качестве вектора нормали к искомой плоскости (P1) можно взять n {–2; 1; 3} – нормаль к (P). Поэтому уравнением (P1) будет –2(x + 4) + 1 (y – 1) +3 (z – 7) = 0, или –2x + y + 3z – 30 = 0.
б) В качестве направляющего вектора искомой прямой (L1) можно взять  q {4; –6; 1} – направляющий вектор (L). Тогда уравнениями (L1) будут
q {4; –6; 1} – направляющий вектор (L). Тогда уравнениями (L1) будут 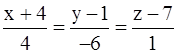 .
.
в) В качестве вектора нормали к искомой плоскости (P2) можно взять q {4; –6; 1} – направляющий вектор (L); и уравнением (P2) будет 4(x + 4) – 6(y – 1) + 1 (z – 7) = 0 или 4x – 6y + z + 15 = 0.
г) Направляющим вектором искомой прямой (L2) можно взять
n { –2; 1; 3} – нормаль к (P). Отсюда получаем уравнения (L2):
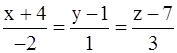 .
.
д) Запишем уравнения (L) в параметрической форме:
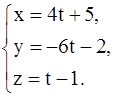
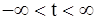 ,
,
Придав t два различных значения, скажем, t = 0 и t = 1, найдём две точки прямой (L):
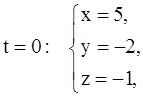 M1(5;–2;–1),
M1(5;–2;–1),
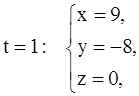 M2(9;–8;0).
M2(9;–8;0).
Точки M, M1, и M2 лежат в искомой плоскости (P3). Составим уравнение (P3) как уравнение плоскости, проходящей через эти три точки:
 2015-06-28
2015-06-28 261
261






