Булевы функции и операции

Рассмотрим возможность представления произвольной функции в виде булевой формулы, содержащей только операции дизъюнкции, конъюнкции и отрицания.

Теоремы 1 и 2 доказывают возможность такого представления. Введем некоторые понятия.

Элементарной конъюнкцией (ЭК) называется выражение 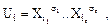где все 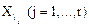– различны, а r – ранг конъюнкции. Функция-константа единица (U_i = 1) считается конъюнкцией нулевого ран­га.

Элементарной дизъюнкцией (ЭД) называется выражение 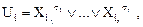где все 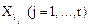– различны, а r – ранг дизъюнкции. Функция-константа единица (U_i = 0) считается дизъюнкцией нулевого ран­га.

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция N = U₁ Ú U₂ Ú...Ú U_k элементарных конъюнкций U₁, U₂,..., U_k. Совершенная ДНФ – частный случай ДНФ, элементарные конъюнкции которой содержат все переменные и ранг их равен n.

Конъюнктивной нормальной формой (КНФ) называется конъюнкция N = U₁ Ù U₂ Ù...Ù U_k элементарных дизъюнкций U₁, U₂,..., U_k. Совершенная КНФ – частный случай КНФ, элементарные дизъюнкции которой содержат все переменные и ранг их равен n.

Теорема 1. Произвольную логическую функцию
f(х₁, х₂,..., х_n) можно представить в виде

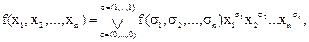(2)

где σ_i Î {0, 1}, x_i⁰ =`х_i, x_i¹ = x_i, σ = (σ₁, …, σ_n) и дизъюнкция берётся по всем n-мерным наборам из нулей и единиц.

Доказательство. Покажем, что левая и правая части соотно­шения (2) совпадают. Подставим в (2) произвольный набор α = (α₁, …, α_n), где каждое α_i Î {0,1}. В левой части по­лучим f(α₁, α₂, …, α_n), а в правой части:

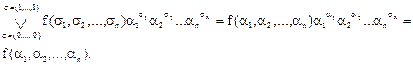Равенства в правой части вытекают из свойств конъюнкции, дизъ­юнкции и из того, что: х^σ = 1 Û х = σ.

Если f(х₁, х₂,..., х_n) ≢ 0, то соотношение (2) можно перепи­сать в форме:

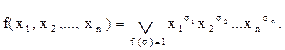(3)

Эта формула (3) называется совершенной дизъюнктивной нормаль­ной формой (СДНФ) функции f(x₁, х₂,..., x_n).

Следствие. Для произвольной логической функции существует взаимнооднозначное соответствие между ее СДНФ и таблицей истинности:

а) СДНФ содержит ровно столько элементарных конъюнкций, сколько единичных наборов у функции;

б) каждому единичному набору σ = (σ₁, …, σ_n) соответствует элементарная конъюнкция всех переменных функции, в которой для σ_i = 0переменная х_iберется с отрицанием и дляσ_i = 1–без отрицания.

Рассмотрим построение СДНФ по таблице истинности функ­ции f(x₁, х₂,..., x_n). Для каждого набора σ = (σ₁, …, σ_n) из единичного множества [1] ( такого, что f(σ₁, …, σ_n) = 1), составляется выражение ЭК: 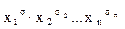. Затем эти конъюнкции соединяются знаком дизъ­юнкции.

Пример 1. Построим СДНФ для функции неэкви­ва­лентности f₇(x₁, х₂)=(х₁ Å х₂). Исходя из единичного мно­жест­ва этой функции [1] = {(0, 1), (1, 0)} формула СДНФ будет иметь вид: F_СДНФ = `х<sub>1</sub> • х<sub>2</sub> Ú х<sub>1</sub>•`х₂.

Теорема 2. Произвольную логическую функцию
f (х₁, х₂,..., х_n) можно представить в виде:

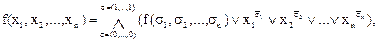(4)

где σ_i Î {0, 1}, х_i⁰ = х_i, x_i¹ = x_i, σ = (σ₁, …, σ_n)

и конъюнкция берётся по всем n-мерным наборам из нулей и единиц.

Доказательство. Из свойства булевой функции имеем
f (х₁, х₂,..., х_n) = 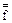(х₁, х₂,..., х_n). Для функции `f(х₁, х₂,..., х_n) по теореме 1 существует представление в виде

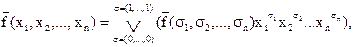
тогда имеем:

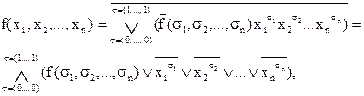
что следует из закона де Моргана.

Заметим также, что 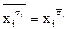. Следовательно,

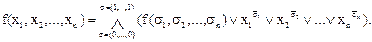
Если f(х₁, х₂,..., х_n) ≢ 1, то соотношение (4) можно переписать в форме

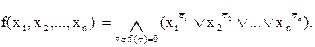(5)

Эта форма называется совершенной конъюнктивной нормальной формой (СКНФ).

Следствие. Для произвольной логической функции также существует взаимнооднозначное соответствие между ее СКНФ и таблицей истинности:

а) СКНФ содержит ровно столько элементарных дизъюнкций, сколько нулевых наборов у функции;

б) каждому нулевому набору σ = (σ₁, …, σ_n) соот­вет­ствует элементарная дизъюнкция всех переменных функции, в которой для σ_i = 1 переменная х_i берется с отрицанием и для σ_i = 0 – без отрицания.

Рассмотрим построение СКНФ по таблице истинности функ­ции f(x₁, х₂,..., x_n). Для каждого набора σ = (σ₁, …, σ_n) из нулевого множества [0] (такого, что f(σ₁, …, σ_n) = 0), составляется выражение ЭД: 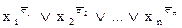. Затем эти дизъюнкции соединяются знаком конъ­юнкции.

Пример 2. Построим СКНФ для функции неэкви­ва­лентности f₇(x₁, х₂) = (х₁ Å х₂). Исходя из нулевого мно­жества этой функции [0] = {(0, 0), (1, 1)} формула СКНФ будет иметь вид: F_СКНФ = (х₁ Ú х₂) • (`х<sub>1</sub> Ú `х₂).