Пусть G(X) – неориентированный граф. Степенью m(х) графа G(X) в вершине х называется число ребер, инцидентных вершине х. Если все числа m(х) для х Î X конечны, то граф называется локально конечным. Петли можно считать одинарным или двойным ребром в зависимости от конкретной задачи.
Обозначим m(хi, xj) = m(xj, хi) – число ребер, соединяющих вершины хi и xj. Если в графе G(X) нет кратных ребер, то m(хi, xj) = 0 или m(хi, xj) = l.
Очевидно, что
m(хi) = 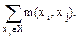
Поскольку каждое ребро учитывается в двух вершинах хi и xj, то общее число ребер m графа G(X):
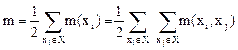 . (7)
. (7)
Это выражение справедливо и для графов с петлями, если петлю считать двойным ребром.
Так как 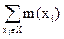 – четное число, то можно сделать вывод о том, что в конечном графе число вершин с нечетной степенью четно. Это следует из того, что если из суммы вычесть все слагаемые, соответствующие вершинам с четной степенью, она останется четной.
– четное число, то можно сделать вывод о том, что в конечном графе число вершин с нечетной степенью четно. Это следует из того, что если из суммы вычесть все слагаемые, соответствующие вершинам с четной степенью, она останется четной.
Граф, степени всех вершин в котором равны, называется однородным, т.е. m(xi) = mn " xi Î X.
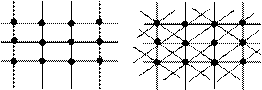
Конечные однородные графы могут быть представлены в виде правильных многогранников: тетраэдра, куба, октаэдра, додекаэдра, икосаэдра и т.д. Примеры бесконечных однородных графов изображены на рис. 3.27.
 |
Из (7) следует, что в однородном графе степени mn, число ребер равно
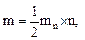 где n - число вершин.
где n - число вершин.
Рис. 3.27. Бесконечные однородные графы
 2015-06-28
2015-06-28 321
321








