Поліноміальні твірні функції

Добуток (1+ 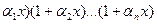породжує r-сполучення, в яких кожен елемент із множини об'єктів { 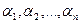} може з'являтися не більш одного разу. Очевидно, для інших типів сполучень варто підібрати й інший вид співмножників.

Якщо об'єкт 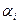може входити в сполучення 0, 1,...,k раз, то замість 1+ 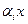треба взяти співмножник 1+ 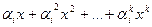(при k=0 співмножник дорівнює одиниці). Тоді при 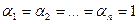коефіцієнти 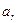багаточлена A(x)=1+ 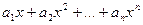являють собою r-сполучення з n різних елементів з повтореннями.

Приклад. Для r-сполучення з трьох елементів a, b, c зі специфікацією {3, 1, 2} маємо (1+x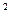+x +x 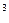)(1+x)(1+x+x 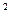)=1+3x+5x 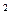+ +6 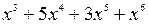. Тут коефіцієнт при 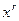дає шукане число r-сполучень. Так, є три 1-сполучення (aaa, aab, aac, abc, acc, bcc), п'ять 4-сполучень (aaab, aaac, aabc, aacc, abcc) і т.д.

Поліноміальна твірна функція (энумератор). Багаточлен вигляду 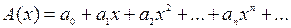називають поліноміальною функцією, або твірною (енумератором) для послідовності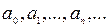

Ця послідовність є r-сполученняз n елементів з повтореннями. Біном Ньютона є функцією, що виробляє для сполучення без повторення. Треба мати на увазі, що змінна x енумератора ніяк не визначена і вважається просто абстрактним символом. Його роль зводиться до того, щоб розрізняти елементи послідовності 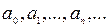При цьому різні перетворення таких послідовностей заміняються відповідними операціями над твірними функціями.

Для сполучення з необмеженими повтореннями елементів n типів енумератор буде (1+х+ 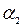+... . 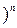Вираження в дужках можна представити у вигляді

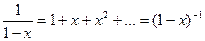
При розгляді виразу (1-х 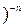як бінома Ньютона з від’ємним показником –n, формально можна записати

,

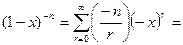
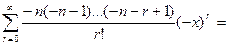
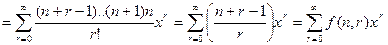що збігається з результатом, отриманим для сполучень. Звідси також слідує формальне відношення

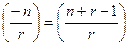
Якщо зажадати, щоб кожен об'єкт входив у сполучення з необмеженими повтореннями парне число раз, то в якості энумератора варто прийняти (1 + x² + x⁴ +...)ⁿ чи

,

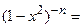
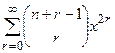тобто число r-сполучень при непарному r дорівнює нулю, а число
2r-сполучень визначається як число r-сполучень без прийнятого раніше обмеження.

Аналогічно визначається енумератор і при інших додаткових умовах. Нехай, наприклад, необхідно визначити число таких r-сполучень з п типів елементів з необмеженими повтореннями, що обов'язково містять хоча б по одному елементу кожного вигляду. Тоді

.

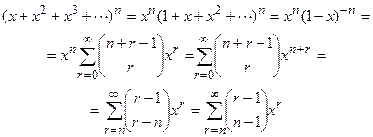Тут при перетворенні суми зроблена заміна змінної n + r на r і використане відношення 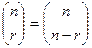зі сполучень. Число шуканих сполучень дорівнює нулю при r < n. і дорівнює C(r — 1, n — 1) при .

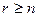Приклад. Для трьох елементів а, b, з існує одне 3-сполучення (abc), число 4 cочетаний дорівнює С(3, 2) = 3 (aabc, abbc, abcc), число 5-сполучень дорівнює С(4, 2) = 6 (aaabc, aabbc, aabcc, abbbc, abbcc, abccc) і т.д.