Основні визначення (продовження)

Визначення. Маршрут (шлях) довжини m визначається як послідовність ребер графу, не обов'язково різних, у яких, що граничні вершини двох сусідніх ребер збігаються.

Замкнутий маршрут приводить до тієї ж вершини, з якої він починається. Маршрут позначається як М = <v₁, v₂,…,v_j,…,v_n>...

Приклад. Неорієнтований граф (рис. 21.1.) і можливі маршрути M¹_{x1 « x4} = <v1, v2, v3, v2, v4, v5>, M² _{x1 « x4}= <v6>

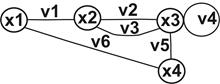
Рис. 15.1. Неорієнтований граф

Визначення. Довжиною маршруту (шляху) М = <v₁, v₂,…,v_j,…,v_n> називається число дуг, що його складують.

Довжина маршруту позначається l(M).

Приклад. Для рис. 15.1. замкнуті маршрути M_{x1 « x1} = <v1, v2, v5, v6>; M¹_{x3 « x3} = < v4>; M² _{x3 « x3}= < v3, v2>.

Визначення. Маршрут, усі ребра якого різні, зветься ланцюгом, маршрут, для якого різні усі вершини, що він проходить, називається простим ланцюгом.

Приклад. Для рис. 15.1. M_{x1 « x1} = <v1, v2, v5, v6> і M_{x1 « x4} = <v1, v2, v4, v5> - ланцюги, M_{x1 « x4} = <v1, v2, v5> - простий ланцюг.

Замкнутий ланцюг звється циклом, замкнутий простий ланцюг називається простим циклом.

Приклад. M_{x1 « x1} = <v1, v2, v4, v5, v6> і M_{x3 « x3} = <v3, v2, v4> - цикли, M_{x1 « x1} = <v1, v2, v5, v6> та M_{x1 « x1} = <v3, v2 > - прості цикли.

Визначення. Цикл графу, що містить усі його ребра, називається ейлеревим циклом.

Визначення. Простий цикл графу, що проходить через усі його вершини, називається гамільтоновим циклом.

Ейлерів і гамільтонів цикли (обходи) можливі не для будь-якого графу чи орграфу. В орграфі при визначенні маршруту, ланцюга, циклу, ейлерева і гамільтонова циклу природно враховується напрямок дуг.

Визначення. Частина графу, що містить поряд з деякою підмножиною ребер і всі інцидентні їм вершини, називається підграфом.

Приклад. Граф G = <X, V>, де X = {x1, x2, x3, x4}, V = {v1, v2, v3, v4, v5} і підграф G' = <X’, V'>, де X’ = { x2, x3, x4}, V' = { v2, v3, v4}, G' Ì G, Х' Ì X, V' Ì V.

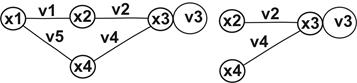
Рис. 15.2. Граф (ліворуч) і підграф (праворуч)

Визначення. Входом чи початковою вершиною орграфу G = <X, V> є вершина x^(s)Î X, у якій p(x^(s)) = 0, виходом чи кінцевою вершиною орграфу G = <X, V> є вершина x^(F)Î X, у якій s(x^(F)) = 0.

Приклад. Початкова вершина x₁ і скінченні вершини x₃, x₅

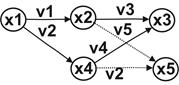
Рис. 15.3. Початкові і скінченні вершини (х1 – вхід, х3, х5 - вихіди)

В орграфу може бути кілька входів чи виходів (х₅ - другий вихід).

У загальному випадку як вхід чи вихід графу можна розглядати довільну (призначену за якім-небудь критерієм) вершину, а саме, якщо умова входу чи виходу не виконуються, тобто `$xi(p(xi) = 0) чи `$xi(s(xi)= = 0), то виводиться фіктивна вершина x^(S)Ï X чи x^(F) Ï X, що з'єднується єдиною дугою до заданої вершини чи единою дугою із заданої вершини.

Приклад. Уведення фіктивних вершин

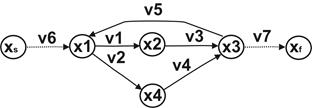
Рис. 15.4. Уведення початкової (вхід x_s) і скінченної (вихід x_f) вершин

Шлях від входу орграфу до його виходу, тобто від вершини x^(S) до його вершини x^(F)називається x^(S) - x^(F) - шляхом. Вважається, що хоча б один такий шлях в орграфі існує.

Якщо в орграфі вершини x_i і x_j зв'язані шляхом M[x_i, x_j], то вершина x_j досяжна з вершини x_i чи що вершина x_i досягає вершини x_j.

Дві вершини графу називаються зв'язними, якщо існує маршрут, що їх з'єднує, інакше - незв'язними.

Визначення. Орграф називається міцно зв’язаним, якщо для будь-якої пари його вершин x_i, x_j Î X існує орієнтований шлях як з x_i у x_j, так і з x_j у x_i.

Визначення. Граф називається зв'язним, якщо для будь-якої пари його вершин x_i, x_j Î X існує шлях з x_i у x_j чи шлях з x_j у x_i.

Визначення. Орграф називається слабо зв’язним, якщо для будь-якої пари його вершин x_i, x_j Î X існує така вершина x_k, що x_k досягає як x_i, так і x_j, чи x_k досяжна як з x_j, так і з x_i.

Визначення. Граф, що не є ні міцно зв’язним, ні зв'язним, ні слабо зв’язним називається незв'язаним графом.

Приклад. Зв'язний граф і міцно зв’язний орграф

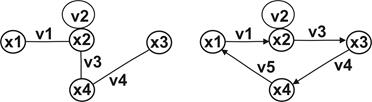
Рис. 15.5. Зв'язаний граф (ліворуч) і міцно зв'язаний орграф (праворуч)

Якщо існує така вершина, видалення якої перетворює зв'язний граф в незв'язаний, то вона називається точкою зчленування, ребро з такими ж властивостями називається мостом.

Визначення. Граф називається нероздільним, якщо він зв'язний і не має точок зчленування, граф, що має хоча б одну точку зчленування є роздільним і називається сепарабельним.

Приклад. Граф з однією точкою зчленування і граф з одним мостом

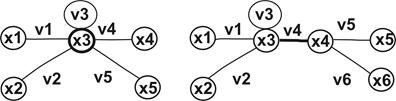
Рис. 15.6. Точка зчленування і міст

Зв'язані ациклічні графи називаються деревами. Дерева містять мінімальну кількість ребер, що забезпечує зв'язаність графу. Незв'язаний граф, компонентами якого є дерева, називається лісом.

Приклад. Дерева з різним розгалуженням

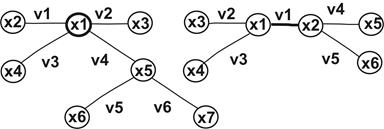
Рис. 15.7. Дерева

Нехай |X| і |V| - кількості вершин і ребер. Для дерев справедливо:

|X| = |V| + 1; |V| = |X| - 1

Визначення. Граф називається плоским (планарним), якщо існує ізоморфний йому граф, що може бути зображений на площині без перетину ребер.

Нехай відстанню d(x₁, x₂) між вершинами x₁, x₂ у дереві (графі) називається довжина мінімального шляху з x₁ у x₂. Відстань від вершини х до найбільш віддаленої від її вершини називається ексцентриситетом е(х) вершини х, тобто

е(х) = max(d(x, y)) = max(È d(x, y))

^{y yÎ X}

Найменший з ексцентриситетів називається радіусом r(T) дерева

r(T) = min(e(x)) = min(Èe(x))

^{x xÎX}

Центральною вершиною дерева Т називається вершина, у якій ексцентрисітет дорівнює радіусу. Центром дерева називається множина його центральних вершин. Кожне дерево має центр, що складається з однієї вершини чи двох суміжних вершин.

Приклад. r(T) = 3, e(x) = 6 графу

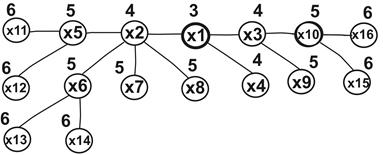
Рис. 15.8. Радіус дерева і ексцентриситети вершин дерева