 |
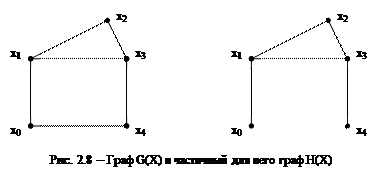
Граф H(x) называется частичным для графа G(X), если все ребра H(X) являются ребрами G(X) и множество вершин графа H(X) совпадает с множеством вершин графа G(X), то есть H(x) Ì G(x) " x Î X (рис.2.8).
Частичный граф содержит часть ребер (дуг). Он также может быть ориентированным или неориентированным в зависимости от исходного.
Отметим, что ноль-граф графа G(X) считается частичным графом каждого графа. Все частичные графы H(X) для G(X) можно получить, выбирая в качестве ребер H(X) всевозможные подмножества множества ребер графа G(X).
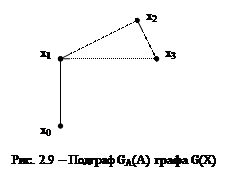 Подграфом GA(A) графа G(X), где A Ì X, называется граф, вершинами которого являются элементы множества A Ì X, а ребрами – все ребра из G, оба конца которых лежат в A (рис.2.9).
Подграфом GA(A) графа G(X), где A Ì X, называется граф, вершинами которого являются элементы множества A Ì X, а ребрами – все ребра из G, оба конца которых лежат в A (рис.2.9).
Таким образом, подграф содержит часть вершин вместе с ребрами, соединяющими эти вершины. Иначе, GA(A) – подграф графа G(X), если A Ì X и GA(x) = G(x) Ç A. Если A = X, то GA(A) = G(X). Для единственной вершины A={a} подграф GA(a) состоит из петель в а. Подграфом GA(A) графа G(X) будет ноль-граф, если A Ì X есть подмножество изолированных вершин графа G(X). Подграф будет ориентированным или неориентированным в зависимости от графа.
Частичным подграфом HA(A), A Ì X графа G(X) называется подграф (рис.2.10), ребрами которого являются некоторые ребра из G(X), оба конца которых лежат в A. Иначе, HA(A) – частичный подграф графа G(X), если A Ì X и HA(x) Ì G(x) Ç A " xÎX.
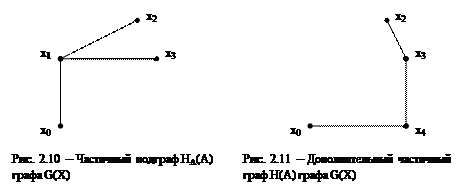
Дополнительным частичным графом H(A) графа G(X) является единственный граф, состоящий из ребер графа G(X), не принадлежащих некоторому частичному подграфу HA(A) графа G(X) (рис.2.11).
Звездным графом, определяемым вершиной х, называется граф, состоящий из всех ребер G(X), имеющих х концевой вершиной. Петли в х могут как включаться, так и не включаться в звездный граф.
 2015-06-28
2015-06-28 912
912








