2015-06-28
504
Функция f (x1,...,xn) называется самодвойственной, если
f (x1,...,xn) =`f (`x1,…,`xn). Например, x,`x – самодвойственные функции, x1x2, x1 ٧ x2 - несамодвойственные.
Лемма 3. Из самодвойственных функций путём суперпозиции можно получить только самодвойственные функции.
Доказательство. Пусть f (y1,...,ym), f1 (x1,...,xn),...,fm (x1,...,xn) - самодвойственные функции. Надо показать, что
Φ (x1,...,xn) = f (f1 (x1,...,xn),..., fm (x1,...,xn)) - самодвойственная.
Из цепочки равенств
`Φ (`x1,…,`xn) =`f (f1 (`x1,…,`xn),…,fm (`x1,…,`xn)) =
`f (`f1 (x1,…,xn),…,`fm (x1,…,xn)) = f (f1(x1,…,xn),…,fm (x1,…,xn)) = 
= Φ (x1,...,xn) следует, что Φ (x1,...,xn) – самодвойственна.
Следствие. Полная система функций должна содержать хотя бы одну несамодвойственную функцию.
Лемма 4. Из несамодвойственной функции подстановкой x и`x можно получить константу.
Доказательство. Функция f (x1,...,xn ) несамодвойственная, поэтому найдется набор a = (a1,...,an)такой, что f (a1,...,a n) = f (`a1,...,`an). По набору a = (a1,...,an) определяются вспомогательные функции
ji (x) (i = 1,2...,n),
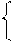x, если ai = 0,
ji (x) =
` x, если ai = 1.
Функция ji (x) обладает свойством ji(0) = ai, ji(1) = `ai.
|
|
|
Рассмотрим функцию j (x) = f (j1(x),..., jn(x)). Она получена из функции f (x1,...,xn) подстановкой x и`x. Функция j (x) – константа, так как 
j (0) = f (j1(0),...,jn(0)) = f (a1,...,an) = f (`a1,...,`an) =
=f (j1(1),..., jn(1)) = j(1).
