Класс линейных функций

Функция f (x₁,...,x_n) называется линейной, если полином этой функции имеет вид

f (x₁,...,x_n) = a₀ Å a₁ x₁ Å...Åa_n x_n , где a_i 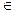{0,1} (i=0,1,...,n).

Например: x,`x – линейны, x₁x₂ - нелинейна.

Лемма 7. Из линейных функций суперпозицией можно получить только линейные функции.

Доказательство очевидно.

Следствие. Полная система функций должна содержать хотя бы одну нелинейную функцию.

Лемма 8. Из нелинейной функции f (x₁,...,x_n), констант 0, 1 и функций x,`x, y суперпозицией можно получить конъюнкцию двух переменных xy.

Доказательство. Так как функция f (x₁,...,x_n) нелинейна, её полином по модулю 2 содержит хотя бы один член с конъюнкцией двух переменных x_i и x_j. Члены полинома, представляющего функцию f (x₁,...,x_n) можно перегруппировать следующим образом:

f (x₁,...,x_n) = x_i x_j f₁ (x₁,...,x_i-1 ,x_i+1,...,x_j-1, x_j+1,..., x_n) Å

Å x_i f₂ (x₁,...,x_i-1, x_i+1,...,x_j-1, x_j+1,..., x_n) Å

Å x_j f₃ (x₁,...,x_i-1, x_i+1,...,x_j-1, x_j+1,..., x_n) Å

Å f₄ (x₁,..., x_i-1 ,x_i+1,..., x_j-1 , x_j+1,..., x_n),

где функция f₁(x₁,..., x_i-1 ,x_i+1,..., x_j-1 , x_j+1,..., x_n) ≢ 0, т.е. существует набор (a₁,..., a _i-1, a _i+1 ,..., a_j-1, a_j+1,..., a_n) такой, что

f (a₁,..., a _i-1, a _i+1 ,..., a_j-1, a_j+1,..., a_n) = 1.

Подставляя этот набор в f (x₁,...,x_n), получим функцию c(x_i, x_j):

c (x_i, x_j) = f (a₁,..., a_i-1, x_i, a_i+1 ,..., a_j-1, x_j, a_j+1,..., a_n) = x_ix_j Å ax_i Å bx_j Å g,

где

a = f₂ (a₁,..., a_i-1, a_i+1,..., a_j-1, a_j+1,..., a_n),

b = f₃ (a₁,..., a_i-1, a_i+1,..., a_j-1, a_j+1,..., a_n),

g = f₄ (a₁,..., a_i-1, a_i+1,..., a_j-1, a_j+1,..., a_n).

Рассмотрим функцию F (x, y) = c (x Åb, y Åa) = xy Å ab Å g.

Она получена суперпозицией c (x_i, x_j), x, y и `x (`x = x Å 1).

Если ab Å g = 0, то F (x, y) = xy,

а если ab Å g = 1, то`F (x, y) = xy.

Критерий полноты системы булевых функций дает теорема 4 (приведем ее без доказательства).

Теорема 4 (о полноте). Для того чтобы система булевых функций {f₁ (x₁₁,..., x_1p1),..., f_s (x_s1,..., x_sps),…} была полна, необходимо и достаточно, чтобы она содержала функцию, не сохраняющую 0; функцию, не сохраняющую 1; несамодвойственную функцию; немонотонную функцию; нелинейную функцию.

Теперь мы можем составить таблицу, отражающую принадлежность каждой из функций двух переменных к рассмотренным классам функций

(табл. 3.6).

Таблица 3.6 – Свойства функций двух переменных

Обозначение функции	Наименование функции	Свойства функции
Сохраняющая 0	Сохраняющая 1	Самодвойственность	Монотонность	Линейность
f1 = 0	Нулевая функция	+	-	-	+	+
f2 = x1 x2	Конъюнкция	+	+	-	+	-
f3 = x1 ® x2	Запрет x1
f4 = x1	Повторение x1
f5 = x2 ® x1	Запрет x2
f6 = x2	Повторение x2
f7 = x1 Å x2	Сложение по |2|
f8 = x1 ٧ x2	Дизъюнкция
f9 = x1 ¯ x2	Стрелка Пирса
f10 = x1 ~ x2	Эквивалентность
f11 =`x2	Отрицание x2
f12 = x2 ® x1	Импликация x2 в x1
f13 =`x1	Отрицание x1
f14 = x1 ® x2	Импликация x1 в x2
f15 = x1 | x2	Штрих Шеффера
f16 = 1	Единичная функция

Эта таблица весьма полезна при выявлении полных систем булевых функций. В ней заполнены только две первых строки. Оставшуюся часть таблицы заполните самостоятельно.