Найти корни уравнения х2 *cos (2х)+ 1 = 0 на отрезке [0;2π]
Для отделения корней построим таблицу значений функции на заданном интервале. Выделим отрезки, на которых функция изменяет знаки.
В таблице выделены диапазоны аргумента, где функция меняет свой знак с + на - или с — на + (рисунок 1). В каждом из этих интервалах находится только один корень уравнения. Для нашего примера это интервалы [1,047; 1,309], [2,094; 2,356], [3,927; 4,189], [5,236; 5,498].
Уточнение корней продемонстрируем на двух методах: методе подбора параметра и методе половинного деления.
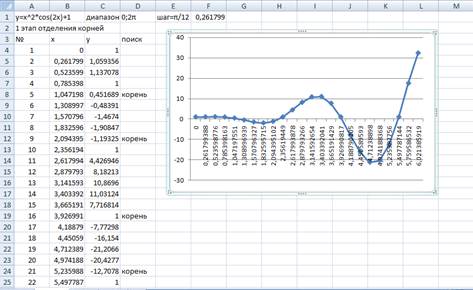
Рисунок 1 - Таблица и график функции к примеру 1
4.1.2 Нахождение корней методом подбора параметра
Корень при помощи подбора параметра находим методом последовательных приближений. Продолжение примера 1
Введем в ячейку А1 значение, являющееся приближением к искомому корню. В нашем случае первым отрезком локализации корня является [1,047; 1,309]. Возьмем за начальное приближение среднюю точку этого отрезка 1,246.
Отведем ячейку (например В1) под функцию, для которой ведется поиск корня. Введем формулу в ячейку В1 (рисунок 2).
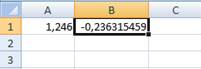
Рисунок 2
Выбираем команду Сервис —> Подбор параметра. На экране появится диалоговое окно Подбор параметра (рисунок 3).
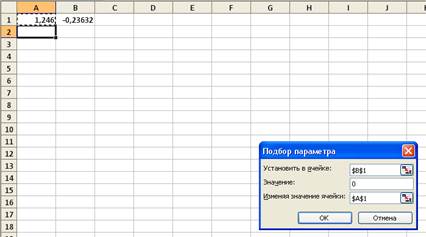
Рисунок 3 – Диалоговое окно Подбор параметра
В поле Установить в ячейке вводим абсолютную ссылку на ячейку В1 (т.е. $В$1). В этом поле указывается ссылка на ячейку, в которой введена формула, вычисляющая значение левой части уравнения. В правой части уравнения при этом переменной быть не должно.
В поле Значение записываем значение правой части уравнения (в нашем случае 0).
В поле Изменяя значение ячейки записываем абсолютный адрес ячейки, содержащую переменную. В нашем случае — $А$1.
Нажимаем ОК.
На экране отображается окно Результат подбора параметра, в котором указывается, что решение найдено. Значения корня и функции соответственно указаны в ячейках А1, В1 (рисунок 4).
В ячейке А1 находится первый корень уравнения — 1,183, в ячейке В1 — значение функции, равное 0,00012.
Аналогично находятся три других корня.
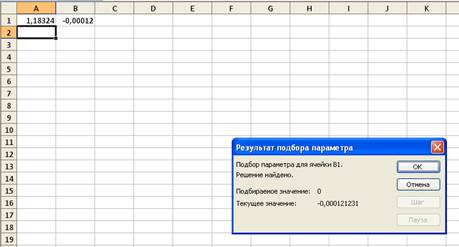
Рисунок 4 - Окно результата подбора параметра
4.1.3 Нахождение корней уравнения методом половинного деления
Алгоритм этого метода сводится к последовательному делению отрезка локализации корня пополам. Процесс деления отрезка продолжается до тех пор, пока его длина не станет меньше 2ε, где ε — точность нахождения корня. В этом случае любая точка отрезка локализации отличается от корня не более чем на ε.
Пусть в качестве первого приближения к корню возьмем середину отрезка [ a;b ], т.е.
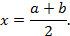
Если F(a) * F(x) < 0, то корень находится в интервале [ а;х ], который берем за новый отрезок локализации корня. Если F(a) * F(x) > 0, то за новый отрезок локализации берем интервал [ х;b ].
Новый отрезок локализации в два раза меньше первоначального. Процесс деления отрезка продолжаем до тех пор, пока его длина не станет меньше 2ε.
Таблица 1 - Вычисление корня методом половинного деления
| Ячейка | Формула либо значение |
| В1 | 0,001 |
| A3 | 2,09 |
| ВЗ | 2,35 |
| СЗ | =(АЗ+ВЗ)/2 |
| D3 | =(A3^2*cos(2*A3)+l)*(C3^2*cos(2*C3)+l) |
| ЕЗ | =C3^2*cos(2*C3)+l |
| F3 | =ЕСЛИ(ВЗ-АЗ<(2* $В$ 1);"Корень найден и равен " &СЗ; "Корень не найден") |
| А4 | =ECJIИ(D3<=0;A3;C3) |
| В4 | =ECJIИ(D3<=0;C3;B3) |
| С4 | =(А4+В4)/2 |
| D4 | =(А4^2 * cos(2 * А4)+1) * (С4^2 * соs(2 * С4)+1) |
| F4 | =ЕСЛИ(В4—А4<(2*$В$ 1);"Корень найден и равен " &С4; "Корень не найден") |
Продолжение примера 1
Пусть в нашем примере требуется найти корни уравнения F(x) = 0 с точностью до 0,001. В качестве примера рассмотрим уточнение корня в интервале [2,09;2,35] Для реализации этого метода напишем последовательность вычислений, введя в ячейки рабочего листа (таблица1) формулы (C3:F4 и А4:В4) и значения (АЗ:ВЗ).
В диапазон C4:F4 формулы вводят не с клавиатуры, а копируя их из диапазона C3:F3. Аналогично копированием заполняется диапазон A5:F11 до тех пор, пока в столбце F не появится надпись — Корень найден и равен и значение найденного корня (рисунок 5).
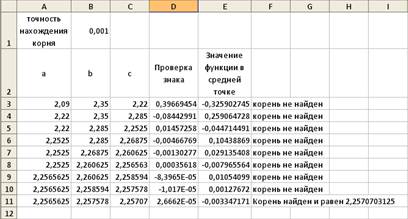
Рисунок 5 - Результаты уточнения корня методом половинного деления
Аналогично находятся все остальные корни уравнения.
4.2 Решение систем нелинейных уравнений графическим методом
Пусть требуется найти решение системы двух нелинейных уравнений. Будем искать его графически с заданной точностью. Графическое решение системы двух уравнений есть точка их пересечения.
Пример 2. Найти графически решение системы уравнений
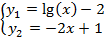
на отрезке [0,2; 3] с шагом 0,2 с точностью 0,001.
Шаг 1. Построим таблицу для х, у1, у2. Столбец х заполним значениями от 0,2 до 3 с шагом, заданном в условии. В столбец у1 введем формулу =LOG10(B7)-2 и растянем до ячейки С21. В столбец у2 введем формулу =-2*В7 + 1 и растянем ее до ячейки D21. Затем с помощью мастера диаграмм строим графики двух функций у1 и у2 (рисунок 6). Определяем визуально точку пересечения графиков и начинаем ее уточнять до заданной точности.
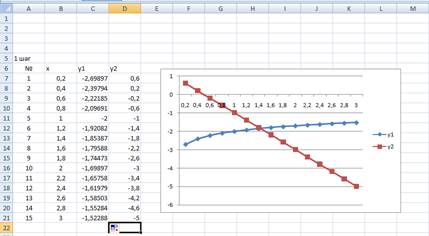
Рисунок 6 - Графическое решение системы нелинейных уравнений (шаг 1)
Шаг 2. Строим новую таблицу, в качестве диапазона для х выбираем диапазон из предыдущего шага, в котором лежит точка пересечения. В нашем примере это диапазон от 1,3 до 1,45. В столбцы у1 и у2 вносим те же формулы, что и на шаге 1, и растягиваем их на весь диапазон значений х. Строим с помощью мастера диаграмм графики и снова визуально определяем точку их пересечения (рисунок 7).
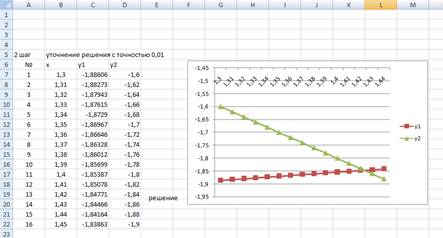
Рисунок 7 - Графическое решение системы нелинейных уравнений (шаг 2)
Повторяя, таким образом, шаги и сужая на каждом шаге интервал по переменной х, определяем координаты точки пересечения графиков с заданной точностью (рисунок 8).
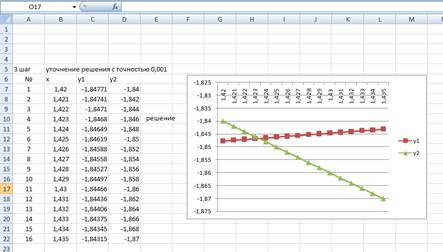
Рисунок 8 - Графическое решение системы нелинейных уравнений (шаг 3)
 2015-06-28
2015-06-28 814
814







