План
1. Вектори у просторі
2. Дії над векторами у просторі
1. У просторі, як і на площині, вектором називається напрямлений відрізок і позначають 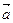 ,
, 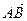 .
.
Нехай вектор 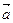 має початком і кінцем точки
має початком і кінцем точки 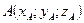 і
і 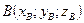 .
.
| Вектори в просторі ^т::••:•;' '/і-'ргй'ї:'. '•. '• {^: у '.•?":•: ••':?': ї:':':^''.":;'::^':^, '.':'•"• '.';Sї^::•:";:^;:•^'"'i*^W?Rll.ЩЩ^;;^^•;^^HЛ<.ll^^^^^ ^•:•^^^f^^y.^^:•::f^.:?:ї'•^^л.^\\'\•v^f:^.їл^v^^.'^fк^i | |
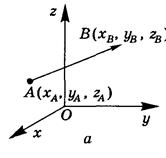 | Координати вектора (рис. а) 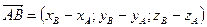 |
Абсолютною величиною (або модулем) вектора називається довжина відрізка, що зображає вектор. Довжина вектора 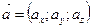 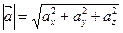 | |
Два вектори називаються рівними, якщо вони суміщаються паралельним перенесенням. Рівність векторів 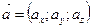 і і 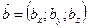 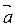 = = 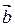 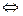 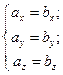 | |
Координати нульового вектора дорівнюють нулю. 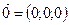 Координати одиничного вектора дорівнюють одиниці. Координати одиничного вектора дорівнюють одиниці. 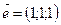 | |
Вектори 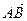 і і 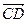 називаються однаково напрямленими, якщо півпрямі називаються однаково напрямленими, якщо півпрямі 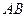 і і 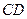 мають однаковий напрямок. мають однаковий напрямок. | |
Два відмінні від нульового вектора називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих. Теорема. У колінеарних векторів відповідні координати пропорційні, і навпаки, якщо у двох векторів відповідні координати пропорційні, то вектори колінеарні. Вектори 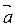 і і 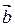 колінеарні, якщо колінеарні, якщо 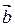 = λ· = λ· 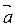 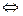 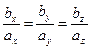 |
2.
| Дії над векторами у просторі ^т::••:•;' '/і-'ргй'ї:'. '•. '• {^: у '.•?":•: ••':?': ї:':':^''.":;'::^':^, '.':'•"• '.';Sї^::•:";:^;:•^'"'i*^W?Rll.ЩЩ^;;^^•;^^HЛ<.ll^^^^^ ^•:•^^^f^^y.^^:•::f^.:?:ї'•^^л.^\\'\•v^f:^.їл^v^^.'^fк^i | |
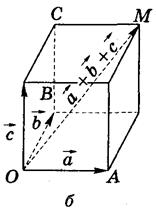 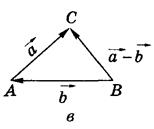 | Сума векторів 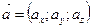 і і 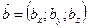 (рис. б) (рис. б) 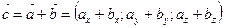 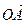 + + 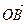 + + 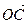 = = 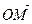 |
Для будь-яких векторів 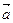 , , 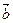 , , 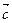 : 1) : 1) 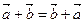 ; 2) ; 2) 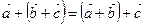 . Якими б не були точки . Якими б не були точки 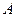 , , 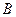 , , 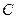 виконується векторна рівність виконується векторна рівність 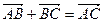 . . | |
Різниця векторів 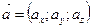 і і 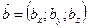 (рис. в) (рис. в) 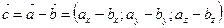 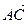 – – 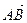 = = 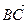 | |
Добуток вектора 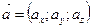 на число на число 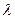 λ· λ· 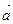 =(λ аx; λ аy; λ аz) =(λ аx; λ аy; λ аz) | |
Скалярним добутком векторів 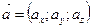 і і 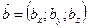 називається число називається число 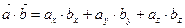 . Теорема. Скалярний добуток векторів дорівнює добутку їх абсолютних величин на косинус кута між ними, тобто . Теорема. Скалярний добуток векторів дорівнює добутку їх абсолютних величин на косинус кута між ними, тобто 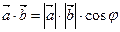 . Властивості скалярного добутку: 1) . Властивості скалярного добутку: 1) 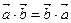 ; 2) ; 2) 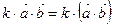 ; 3) ; 3) 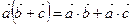 . . | |
Кут між векторами 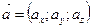 і і 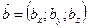 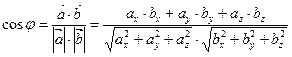 Теорема. Теорема. 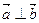 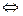 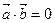 . . |
 2015-06-28
2015-06-28 1668
1668