Векторное n-мерное пространство

Пусть дана прямоугольная декартова система координат в пространстве.

Если все векторы в этом пространстве привести к общему началу в точке О (0,0,0), то координаты всех векторов совпадут с координатами их концов. Поэтому можно считать, что упорядоченные тройки вещественных чисел задают точки (или векторы) пространства. Их называют трехмерными точками (векторами).

Трехмерным векторным пространством будем называть множество всех упорядоченных троек вещественных чисел

(трехмерных векторов, трехмерных точек). Такое пространство принято обозначать R³.

По аналогии с трехмерным векторным (точечным) пространством вводится понятие n -мерного векторного пространства.

Зададим натуральное число n.

Упорядоченную совокупность n вещественных чисел будем называть n -мерным вектором ( n -мерной точкой), а сами числа - его координатами (компонентами).

Множество всех n -мерных векторов будем называть n -мерным векторным (точечным) пространством и обозначим

его Rⁿ. Числовая прямая (R¹) и координатная плоскость (R²) являются частными случаями такого пространства.

Понятие равенства, сложения, вычитания, умножения на скаляр и скалярного произведения с n- мерными векторамивведем аналогично соответствующим операциям с трехмерными векторами в координатной форме. Отсюда следует, что сумма двух n -мерных векторов и произведение n -мерного вектора на скаляр тоже являются n -мерными векторами

Пространство L называют линейным, если сложение элементов и умножение их на скаляр дает элемент того же пространства и при этом обладают свойствами:

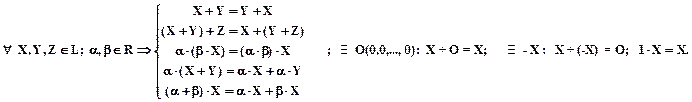
Вектор О называют нулевым, а вектор -Х -противоположным вектору Х.

Векторное n -мерное пространство R ⁿ является линейным.

Примеры линейных пространств:

- множество всех вещественных чисел,

- множество всех многочленов не выше пятой степени с вещественными

коэффициентами,

- множество всех матриц одинаковой размерности.

По аналогии с трехмерным пространством будем считать, что скалярный квадрат вектора равен квадрату его длины.

Длину n- мерного вектора будем обозначать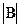, тогда .

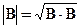Векторное n- мерное пространство, в котором введено понятие скалярного произведения (длины вектора) будем называть евклидовым пространством.

Пусть даны n -мерные векторы

и вещественные числа х₁, х₂,..., х_j,... х_k, которые будем называть коэффициентами.

Линейной комбинацией данных векторов назовем n- мерный вектор В, определяемый равенством:

.

Если коэффициенты являются переменными величинами, то координаты вектора В тоже будут переменными.

Векторы А₁, А₂,..., А_к будем называть линейно независимыми, если их линейная комбинация равна нулевому вектору

( В=О ) только, когда все коэффициенты равны нулю. В противном случае векторы называют линейно зависимыми.

6.1. Равенство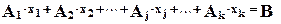

эквивалентно системе 5.3., у которой количество неизвестных равно k.

6.2. Максимальное количество линейно независимых n- мерных векторов равно n.

6.3. Если среди векторов содержится нулевой вектор, то они линейно зависимы.

6.4. Условие линейной зависимости векторов