Арифметическое пространство. Векторы и операции над ними. Линейная зависимость векторов. Базис

Важнейшим примером линейного пространства является так называемое арифметическое (покомпонентное) пространство. Векторами этого пространства называются упорядоченные совокупности из 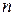вещественных (комплексных) чисел, которые называются компонентами вектора. Основным представителем здесь являются вектор-столбец (основной случай; далее вместо термина «вектор-столбец» используется термин «вектор»). Векторы обозначаются одним символом , т.е. имеет место запись:

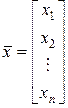– вектор-столбец. (2.1.1)

Число 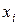называется 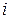-ой компонентой вектора, 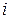– номер компоненты.

Само арифметическое пространство в вещественном случае далее будем обозначать 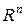, а в комплексном – .

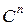Два вектора арифметического пространства считаются равными в том и только в том случае, если равны их соответствующие компоненты. Действия сложения и умножения на число определяются покомпонентно:

– сложение по правилу

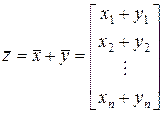; (2.1.2)

– умножение вектора на число по правилу

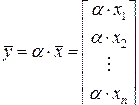. (2.1.3)

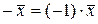Противоположным вектором для вектора является вектор . Роль нулевого вектора играет вектор, все компоненты которого равны нулю, т.е.

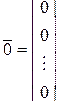– нулевой вектор. (2.1.4)

Арифметическое пространство может быть построено также и на основе вектор-строки:

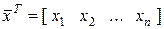– вектор-строка, (2.1.5)

где «^T» – знак матричного транспонирования.

Для вектор-строки соответствующие операции определяются аналогично.

Линейной комбинацией векторов , , 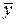…, 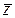будем называть сумму произведений этих элементов на произвольные вещественные числа, т.е. выражение вида

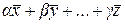(2.1.6)

где 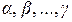– произвольные числа.

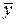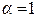В частности, на основании (2.1.6) для пары векторов ,(при и 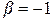) можем определить операцию вычитания векторов:

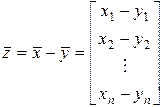. (2.1.7)

Линейно зависимыми векторами , , 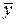…, 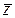называются векторы, для которых найдутся такие числа 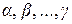, из которых хотя бы одно отлично от нуля, при этом линейная комбинация векторов , , 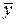…, 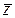с указанными числами является нулевым вектором, т.е.:

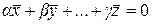. (2.1.8)

Линейно независимыми векторами , , 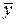…, 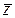называются векторы, если их линейная комбинация (2.1.6) является нулевым вектором лишь при условии .

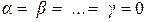Сформулируем без доказательства ряд утверждений.

1. Для того, чтобы векторы , , 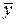…, 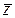были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов являлся линейной комбинацией остальных элементов.

2. Если среди векторов , , 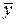…, 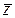имеется нулевой вектор, то эти элементы линейно зависимы.

Единичным вектором в 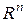называется вектор 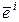, i -ая компонента которого равна единице, остальные нули, т.е.

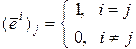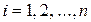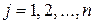, ; . (2.1.9)

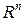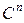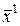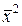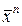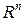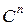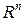Базисом пространства () называется совокупность линейно независимых векторов , , …, пространства (), если для каждого вектора пространства найдутся вещественные (комплексные) числа 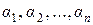такие, что справедливо равенство

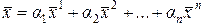. (2.1.10)

Например, 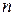единичных векторов 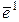, , 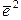…, 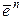образуют базис в .

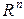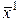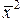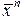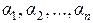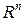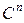Равенство (2.1.10) называется разложением вектора по базису , , …, , а числа называются коэффициентами этого разложения. Каждый вектор пространства () может быть разложен по базису 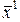, , 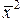…, 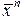единственным способом, т.е. коэффициенты разложения каждого вектора 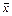по базису 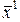, , 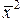…, 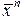определяется однозначно.