1. Вибрати довільні вектори 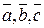 . Зобразити на рисунку їхні лінійні комбінації:
. Зобразити на рисунку їхні лінійні комбінації:
1.1. 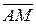 , ,
| 1.2. 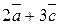 , ,
| 1.3. 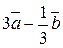 , ,
|
1.4. 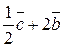 , ,
| 1.5. 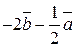 , ,
| 1.6. 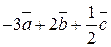 . .
|
2. Показати, що вектори 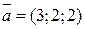 ,
, 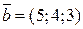 ,
, 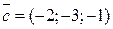 утворюють базис у просторі. Знайти координати вектора
утворюють базис у просторі. Знайти координати вектора 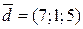 в цьому базисі.
в цьому базисі.
3. Задано точки 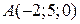 ,
, 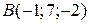 ,
, 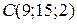 ,
, 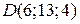
Знайти:
3.1. координати векторів 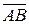 ,
, 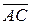 ,
, 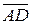 та їхні модулі.
та їхні модулі.
3.2. координати, модуль і напрямні косинуси вектора 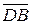 .
.
3.3. координати лінійної комбінації векторів 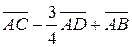 .
.
3.4. довжину медіани 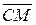
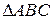 .
.
3.5. орт вектора 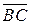 .
.
3.6. координати точки 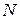 , яка ділить відрізок між точками
, яка ділить відрізок між точками 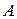 і
і 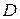 у відношенні
у відношенні 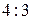 .
.
3.7. координати центра мас однорідного стержня, кінці якого розміщено в точках 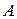 і
і 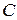 .
.
3.8. скалярний добуток векторів 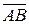 і
і 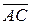 .
.
3.9. внутрішній кут 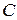 і зовнішній кут
і зовнішній кут 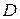
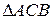 .
.
3.10. проекцію вектора 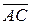 на вектор
на вектор 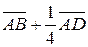 .
.
3.11. роботу, яку виконує сила 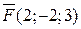 , якщо точка її прикладання, рухаючись прямолінійно, переміщується з точки
, якщо точка її прикладання, рухаючись прямолінійно, переміщується з точки 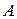 в точку
в точку 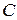 .
.
3.12. площу 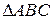 .
.
3.13. синус кута 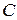
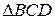 .
.
3.14. координати вектора 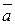 , ортогонального двом векторам
, ортогонального двом векторам 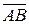 і
і 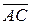 , якщо
, якщо 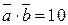 ,
, 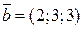 .
.
3.15. момент сили 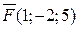 , прикладеної до точки
, прикладеної до точки 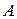 відносно точки
відносно точки 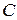 .
.
3.16. об’єм піраміди 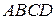 .
.
3.17. довжину висоти 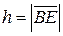 піраміди з вершинами в точках
піраміди з вершинами в точках 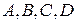 .
.
|
|
|
З’ясувати:
3.18. чи виконується необхідна і достатня умова перпендикулярності векторів 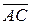 і
і 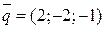 ?
?
3.19. при яких 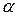 і
і 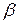 вектори
вектори 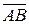 і
і 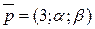 колінеарні?
колінеарні?
3.20. чи лежать точки 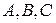 і
і 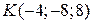 в одній площині?
в одній площині?
3.21. якою трійкою (правою чи лівою) є трійка 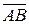 ,
, 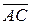 ,
, 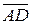 ?
?
3.22. чи компланарні вектори 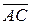 ,
, 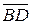 і
і 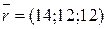 ?
?
4. Вектор 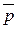 перпендикулярний до векторів
перпендикулярний до векторів 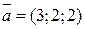 і
і 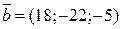 утворює з віссю
утворює з віссю 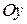 тупий кут. Знайти його координати, якщо
тупий кут. Знайти його координати, якщо 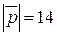 .
.
 2015-06-28
2015-06-28 173
173








