Вектор 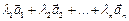 , где
, где 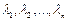 – произвольные действительные числа, называется линейной комбинацией векторов
– произвольные действительные числа, называется линейной комбинацией векторов 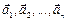 .
.
Система векторов 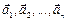 линейно зависима, если, по крайней мере, один из них является линейной комбинацией остальных. В противном случае линейно независимы. Например, если
линейно зависима, если, по крайней мере, один из них является линейной комбинацией остальных. В противном случае линейно независимы. Например, если 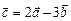 , то векторы
, то векторы 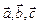 линейно зависимы.
линейно зависимы.
Любые 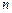 линейно независимых векторов пространства
линейно независимых векторов пространства 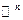 называют базисом этого пространства. Если эти векторы единичные и попарно перпендикулярные, то базис называется ортонормированным.
называют базисом этого пространства. Если эти векторы единичные и попарно перпендикулярные, то базис называется ортонормированным.
Базис на плоскости (в 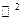 ) образуют любые два неколлинеарные вектора ) образуют любые два неколлинеарные вектора 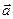 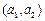 и и 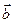 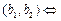 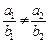 | Ортонормированный базис в 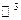 - - 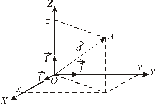 три попарно перпендикулярных единичных вектора три попарно перпендикулярных единичных вектора 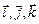 : : 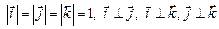 Разложение вектора по базису Разложение вектора по базису 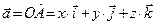 , , 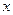 , , 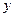 , , 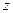 – координаты вектора. Обозначение: – координаты вектора. Обозначение: 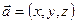 |
Базис в пространстве (в 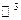 ) образуют любые три некомпланарных вектора ) образуют любые три некомпланарных вектора 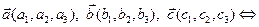 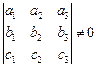 |
| Проекция вектора на ось | Прямоугольная декартова система координат (ПДСК) | |
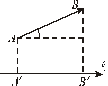 пр пр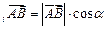 | 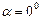 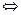 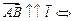 пр пр 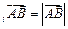 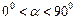 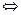 пр пр 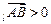 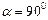 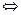 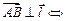 пр пр 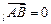 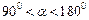 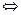 пр пр 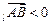 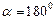 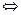 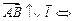 пр пр 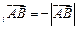 | 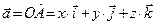 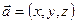 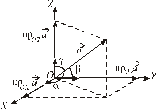 , , 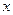 – абсцисса, – абсцисса, 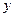 – ордината, – ордината, 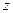 – аппликата. – аппликата. |
В ПДСК: 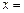 пр
пр 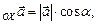
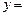 пр
пр 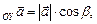
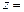 пр
пр 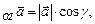 где
где 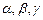 – углы, которые составляет вектор
– углы, которые составляет вектор 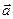 с координатными осями
с координатными осями 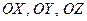 соответственно;
соответственно; 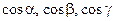 называются направляющими косинусами вектора
называются направляющими косинусами вектора 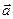 :
: 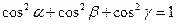 .
.
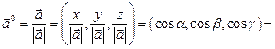 единичный вектор, сонаправленный с вектором
единичный вектор, сонаправленный с вектором 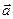 ,– орт вектора
,– орт вектора 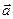
(нормированный вектор).
Если даны точки А 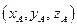 и В и В 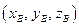 , то , то | ||
координаты вектора 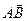 | координаты середины М отрезка АВ | длина отрезка АВ (модуль вектора 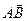 ) ) |
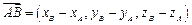 | 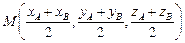 | 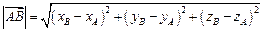 |
Если векторы заданы координатами 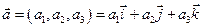 и и 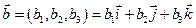 , то , то | |||
| модуль вектора | Линейные операции | Равенство векторов | Коллинеарность |
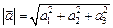 | 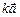 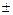 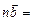 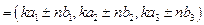 | 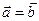 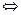 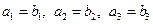 | 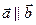 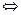 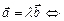 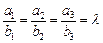 |
Скалярное произведение двух векторов ( обозначение: 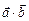 или
или 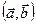 )
)
| По определению | В проекцииях | В координатах | Свойства |
Число, равное 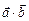 = = 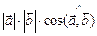 | 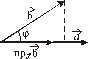 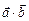 = = 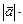 пр пр 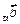 = = 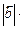 пр пр 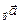 | 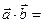 = = 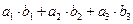 | 1) 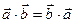 ; 2) ; 2) 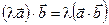 ; 3) ; 3) 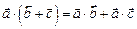 ; 4) ; 4) 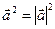 ; 5) ; 5) 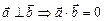 . . |
 2015-06-28
2015-06-28 897
897








