Решение уравнений в кольце остатков по данному модулю

Сравнение 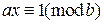всегда имеет решение, если числа a и b взаимно просты.

Это следует из того, что выражение ax-by = 1 – это линейное представление наибольшего общего делителя a и b.

Такую задачу иногда формулируют в виде: найти 1/ a в кольце вычетов по модулю b. В самом деле, выражение ax = 1 означает по сути то же самое, что x = 1/ a (x – искомая величина).

В некоторых случаях вычисляют c / a в кольце вычетов по модулю b. В этом случае сначала можно вычислить 1/a, затем умножить результат на c в кольце вычетов по модулю b.

Уточняем, что умножить число в кольце вычетов по модулю b означает сначала умножить число, затем заменить результат его остатком от деления на b.

Пример

Можно решить уравнение 7x = 1 в кольце вычетов по модулю 9, то есть провести вычисление 1/7 в Z₉.

В данном случае обозначим неизвестную величину как х.

Тогда x = 1/7 в Z₉ Û

7x º 1 (mod 9) Û

7x – 1 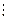9 Û

7x – 1 = 9y Û

7x – 9y = 1

Мы получили уже знакомую нам ситуацию – линейное диофантово уравнение.

Можем его решить, но для первоначальной задачи достаточно найти всего одно значение х – например, подойдёт x = 4. Заметим, что это число находится в пределах от 0 до 8, поэтому может быть остатком при делении на 9.

Итак, ответ: x = 4.

Примечание. Ответ легко проверить умножением: 4 х 7 при делении на 9 даёт остаток 1.

Если бы мы искали, например, 5/7 в Z₉, то сначала нашли бы сначала 1/7 в Z₉ (получив число 4), а затем домножили бы это число на 5 и взяли бы остаток при делении на 9 (остаток от деления 20 на 9 равен 2).

В этом случае ответ был бы равен 2.

Примечание. В задачах на нахождение выражений вида a/b в кольце вычетов по модулю c ответ всегда единственный, и является целым числом, находящимся в пределах от 0 до (c - 1).

В некоторых случаях деление невозможно, поскольку не каждое диофантово уравнение имеет решение. Например, уравнение 4x º 1 (mod 10) не имеет решений, поскольку 4x – чётное число, и при делении на 10 остаток будет чётным.