Определение. Функцию от одной или нескольких переменных, аргументы и значение которой могут принимать только значения 0 или 1, называют булевой функцией (в честь английского математика Джорджа Буля (1815 - 1864), одного из основателей математической логики).
Примеры.
Конъюнкция: 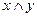 = 1 тогда и только тогда, когда x и y оба равны 1.
= 1 тогда и только тогда, когда x и y оба равны 1.
Дизъюнкция: 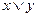 = 1 тогда и только тогда, когда x и y оба равны 1.
= 1 тогда и только тогда, когда x и y оба равны 1.
Для того, чтобы каждый раз не описывать значения словами, булеву функцию обычно задают таблицей истинности, то есть таблицей, в которой указаны значения для всех наборов переменных.
При этом значения наборов переменных располагают в лексикографическом порядке. Сначала набор из одних нулей, затем правый ноль заменяют 1, и так далее, до набора из одних единиц. Например:
| x | y | 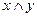
|
| x | y | 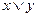
|
Эквивалентность: 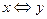 (Значение выражения равно 1, если значения x и y совпадают)
(Значение выражения равно 1, если значения x и y совпадают)
| x | y | 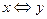
|
Симметрическая разность: 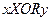 (Значение выражения равно 1, если значения x и y не совпадают)
(Значение выражения равно 1, если значения x и y не совпадают)
| x | y | 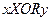
|
Импликация: 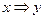 (Мнемоническое правило: из нуля следует что угодно – и ноль, и единица)
(Мнемоническое правило: из нуля следует что угодно – и ноль, и единица)
| x | y | 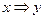
|
Отрицание: 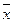
| x | 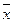
|
 2015-06-28
2015-06-28 579
579







