2015-06-28
2202
Пусть r Í Х х Y.
Функциональное отношение – бинарное отношение r, для которого
" х Î Dr $! y Î Y: х r y.
Всюду определённое отношение – бинарное отношение r, для которого Dr =Х ("нет одиноких х ").
Сюръективное отношение – бинарное отношение r, для которого Jr = Y ("нет одиноких y ").
Инъективное отношение – бинарное отношение, в котором разным х соответствуют разные у.
Биекция – функциональное, всюду определённое, инъективное, сюръективное отношение, задаёт взаимно однозначное соответствие множеств.
Например:
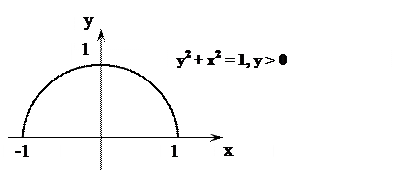Пусть r = { (x, y) Î R2 | y2 + x2 = 1, y > 0 }.
Отношение r - функционально,
не всюду определено ("есть одинокие х "),
не инъективно (есть разные х, которым соответствуют одинаковые у),
не сюръективно ("есть одинокие у "),
не биекция.
Например:
Пусть Ã= {(x,y) Î R2 | y = x+1}
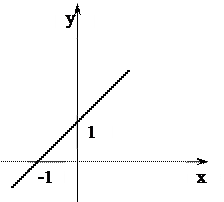
Отношение Ã- функционально,
Отношение Ã- всюду определено ("нет одиноких х "),
Отношение Ã- инъективно (нет разных х, которым соответствуют одинаковые у),
Отношение Ã- сюръективно ("нет одиноких у "),
Отношение Ã- биективно, взаимно-однородное соответствие.
Например:
Пусть j={(1,2), (2,3), (1,3), (3,4), (2,4), (1,4)} задано на множестве N4.
Отношение j - не функционально, x=1 соответствует три y: (1,2), (1,3), (1,4)
Отношение j - не всюду определенно D j={1,2,3}¹ N4
Отношение j - не сюръективно I j={1,2,3}¹ N4
Отношение j - не инъективно, разным x соответствуют одинаковые y, например (2,3) и (1,3).
Задание к лабораторной работе
1. Заданы множества N1 и N2. Вычислить множества:
(N1 х N2) Ç (N2 х N1);
(N1 х N2) È (N2 х N1);
(N1 Ç N2) x (N1 Ç N2);
(N1 È N2) x (N1 È N2),
где N1 = { цифры номера зачетной книжки, три последние };
N2 = { цифры даты и номера месяца рождения }.
2. Отношения r и g заданы на множестве N6={1,2,3,4,5,6}.
Описать отношения r, g, r -1, r ○ g, r- 1 ○ g списком пар.
Найти матрицы отношений r и g.
Для каждого отношения определить область определения и область значений.
Определить свойства отношений.
Выделить отношения эквивалентности и построить классы эквивалентности.
Выделить отношения порядка и классифицировать их.
1) r = { (m, n) | m > n }
g = { (m, n) | сравнение по модулю 2 }
2) r = { (m, n) | (m - n) делится на 2 }
g = { (m, n) | m делитель n }
3) r = { (m, n) | m < n }
g = { (m, n) | сравнение по модулю 3 }
4) r = { (m, n) | (m + n) - четно }
g = { (m, n) | m2=n }
5) r = { (m, n) | m / n -степень 2 }
g = { (m, n) | m = n }
6) r = { (m, n) | m / n -четно }
g = { (m, n) | m ³ n }
7) r = { (m, n) | m / n -нечетно }
g = { (m, n) | сравнение по модулю 4 }
8) r = { (m, n) | m * n -четно }
g = { (m, n) | m £ n }
9) r = { (m, n) | сравнение по модулю 5 }
g = { (m, n) | m делится на n }
10) r = { (m, n) | m - четно, n - четно }
g = { (m, n) | m делитель n }
11) r = { (m, n) | m = n }
g = { (m, n) | (m + n) £ 5 }
12) r = { (m, n) | m и n имеют одинаковый остаток от деления на 3 }
g = { (m, n) | (m - n) ³2 }
13) r = { (m, n) | (m + n) делится нацело на 2 }
g = { (m, n) | 2 £ (m - n) £4 }
14) r = { (m, n) | (m + n) делится нацело на 3 }
g = { (m, n) | m ¹ n }
15) r = { (m, n) | m и n имеют общий делитель }
g = { (m, n) | m 2 £ n }
16) r = { (m, n) | (m - n) делится нацело на 2 }
g = { (m, n) | m < n +2 }
17) r = { (m, n) | сравнение по модулю 4 }
g = { (m, n) | m £ n }
18) r = { (m, n) | m делится нацело на n }
g = { (m, n) | m ¹ n, m- четно }
19) r = { (m, n) | сравнение по модулю 3 }
g = { (m, n) | 1 £ (m - n) £3 }
20) r = { (m, n) | (m - n) делится нацело на 4 }
g = { (m, n) | m ¹ n }
21) r = { (m, n) | m - нечетно, n - нечетно }
g = { (m, n) | m £ n, n- четно }
22) r = { (m, n) | m и n имеют нечетный остаток от деления на 3 }
g = { (m, n) | (m - n) ³1 }
23) r = { (m, n) | m * n -нечетно }
g = { (m, n) | сравнение по модулю 2 }
24) r = { (m, n) | m * n -четно }
g = { (m, n) | 1 £ (m - n) £3 }
25) r = { (m, n) | (m + n) - четно }
g = { (m, n) | m не делится нацело на n }
26) r = { (m, n) | m = n }
g = { (m, n) | m делится нацело на n }
27) r = { (m, n) | (m - n)- четно }
g = { (m, n) | m делитель n }
28) r = { (m, n) | (m - n) ³2 }
g = { (m, n) | m делится нацело на n }
29) r = { (m, n) | m 2 ³ n }
g = { (m, n) | m / n -нечетно }
30) r = { (m, n) | m ³ n, m -четно }
g = { (m, n) | m и n имеют общий делитель, отличный от 1 }
3. Определить является ли заданное отношение f -функциональным, всюду определенным, инъективным, сюръективным, биекцией (R - множество вещественных чисел). Построить график отношения, определить область определения и область значений.
Выполнить это же задание для отношений r и g из пункта 3 лабораторной работы.
1) f={ (x, y) Î R 2 | y=1/x +7x }
2) f={ (x, y) Î R 2 | x ³ y }
3) f={ (x, y) Î R 2 | y ³ x }
4) f={ (x, y) Î R 2 | y ³ x, x ³ 0 }
5) f={ (x, y) Î R 2 | y2 + x2 = 1 }
6) f={ (x, y) Î R 2 | 2 | y | + | x | = 1 }
7) f={ (x, y) Î R 2 | x + y £ 1 }
8) f={ (x, y) Î R 2 | x = y2 }
9) f={ (x, y) Î R 2 | y = x3 + 1}
10) f={ (x, y) Î R 2 | y = -x2 }
11) f={ (x, y) Î R 2 | | y | + | x | = 1 }
12) f={ (x, y) Î R 2 | x = y -2 }
13) f={ (x, y) Î R 2 | y2 + x2 ³ 1, y > 0 }
14) f={ (x, y) Î R 2 | y2 + x2 = 1, x > 0 }
15) f={ (x, y) Î R 2 | y2 + x2 £ 1, x > 0 }
16) f={ (x, y) Î R 2 | x = y2, x ³ 0 }
17) f={ (x, y) Î R 2 | y = sin(3x + p) }
18) f={ (x, y) Î R 2 | y = 1 /cos x }
19) f={ (x, y) Î R 2 | y = 2| x | + 3 }
20) f={ (x, y) Î R 2 | y = | 2x + 1| }
21) f={ (x, y) Î R 2 | y = 3x }
22) f={ (x, y) Î R 2 | y = e-x }
23) f ={ (x, y) Î R 2 | y = e| x | }
24) f={ (x, y) Î R 2 | y = cos(3x) - 2 }
25) f={ (x, y) Î R 2 | y = 3x2 - 2 }
26) f={ (x, y) Î R 2 | y = 1 / (x + 2) }
27) f={ (x, y) Î R 2 | y = ln(2x) - 2 }
28) f={ (x, y) Î R 2 | y = | 4x -1| + 2 }
29) f={ (x, y) Î R 2 | y = 1 / (x2+2x-5)}
30) f={ (x, y) Î R 2 | x = y3, y ³ - 2 }.
Контрольные вопросы
1.Декартово или прямое произведение множеств.
2.Определение бинарного отношения.
3.Способы описания бинарных отношений.
4.Область определения и область значений.
5.Свойства бинарных отношений.
6.Отношение эквивалентности и классы эквивалентности.
7.Отношения порядка: строгого и нестрого, полного и частичного.
8.Классы вычетов по модулю m.
9.Функциональные отношения.
10. Инъекция, сюръекция, биекция.
Лабораторная работа № 3
