Свойства бинарных отношений. Пусть rзадано на множестве X, r Í Х2

Пусть r задано на множестве X, r Í Х²

Рефлексивность: " х Î Х х r х.

Антирефлексивность: 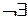х Î Х х r х.

Нерефлексивность: $ х Î Х (x, x) Ï r.

Симметричность: " х, y Î Х х r y => y r х.

Антисимметричность: " х, y Î Х х r y, y r х Û x = y.

Транзитивность: " х, y, z Î Х х r y, y r z => x r z.

Отношение порядка – антисимметрично, транзитивно.

Отношение нестрого порядка (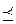) - рефлексивно,
антисимметрично,
транзитивно.

Отношение строгого порядка (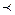) - антирефлексивно,
антисимметрично,
транзитивно.

В отношениях полного порядка все элементы сравнимы между собой, а в отношениях частичного порядка не все элементы сравнимы между собой.

Отношение эквивалентности (~) - рефлексивно,
симметрично,
транзитивно.

Класс эквивалентности для х: [ x ] = { y Î Х | x ~ y }.

Обратное отношение получается путём перестановки значений в парах исходного отношения.

Композиция отношений r и g -отношение, состоящее из пар
r ○ g = { (x, z)| х r у, y g z }

Например:

Отношения r и g заданы на множестве Х = {1, 2, 3, 4, 5, 6,}.

r= {(1,4), (2,5), (3,6), (4,1), (6,3)},

g = {(1,1), (2,3), (3,4), (4,5), (5,6), (6,6)}.

Область определения D_r= {1, 2, 3, 4, 6}.

Область значений J _r= {1, 3, 4, 5, 6}.

Обратное отношение r^-1 = {(4,1), (5,2), (6,3), (1,4), (3,6)}.

Отношение r- антирефлексивно, не симметрично, не транзитивно.

Область определения D_g= {1, 2, 3, 4, 5, 6}.

Область значений J _g= {1, 3, 4, 5, 6}.

Отношение g- не рефлексивно, антисимметрично, не транзитивно.

Композиция r ○ g = {(1,5), (2,6), (3,6), (4,1), (6,4)}.

Например:

Отношение r= { (x, y) | сравнение по модулю m, x,y Î N }.

Отношение сравнения по модулю m на множестве натуральных чисел:x = y mod m, что означает x и y имеют одинаковый остаток при делении на m (классы вычетов по модулю m).

Отрезок натурального ряда N₄={1,2,3,4}.

Отношение сравнения по модулю 2 на N₄ :

d = { (1,1),(1,3),(2,2),(2,4),(3,1),(3,3),(4,2),(4,4)}.

Область определения D_d = {1, 2, 3, 4}.

Область значений J _d = {1, 2, 3, 4}.

Отношение d - рефлексивно, симметрично, транзитивно.

Отношение d - отношение эквивалентности.

Классы эквивалентности: [ 1 ]={ 1,3 }=[ 3 ]

[ 2 ]={ 2,4 }=[ 4 ].

Например:

Отношения j и n заданы на множестве N_4.

j ={ (1,2), (2,3), (1,3), (3,4), (2,4), (1,4) }

n={ (1,1),(2,2),(3,3),(4,4) }.

Область определения D_j = { 1, 2, 3 }.

Область значений J _j = { 2, 3, 4 }.

Отношение j - антирефлексивно, антисимметрично, транзитивно.

Отношение j - отношение строгого порядка.

Область определения D_n = { 1, 2, 3,4 }.

Область значений J _n = { 1, 2, 3, 4 }.

Отношение n - рефлексивно, симметрично, антисимметрично, транзитивно.

Отношение n - отношение нестрогого частичного порядка.

Отношение n - отношение эквивалентности.

Классы эквивалентности: [ 1 ]={ 1}

[ 2 ]={ 2 }

[ 3 ]={ 3 }

[ 4 ]={ 4 }.