Функции не сохраняют 0,
g- сохраняет 1,
Функции не монотонные, и не самодвойственные.
Проверим на линейность (составим многочлены Жегалкина).
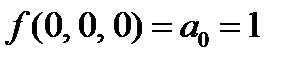
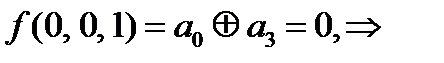
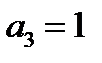
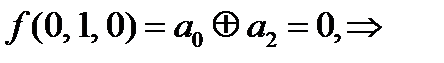
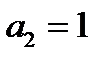
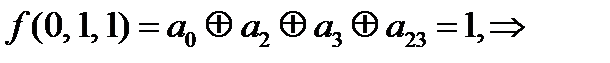
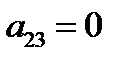
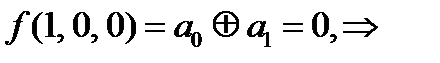
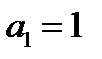
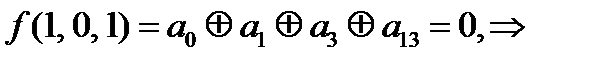
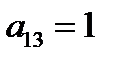
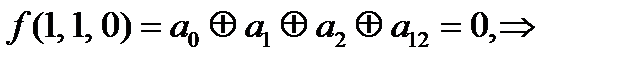
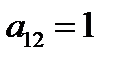
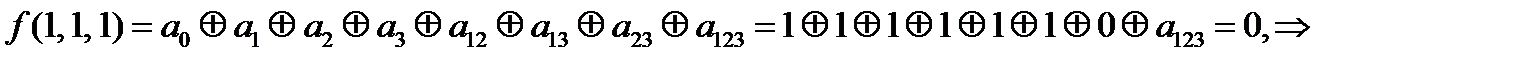
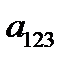 =0
=0
Следовательно, функция 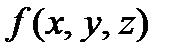 представляется многочленом Жегалкина
представляется многочленом Жегалкина
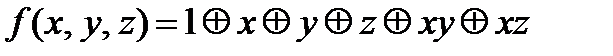
Нелинейная.
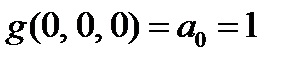
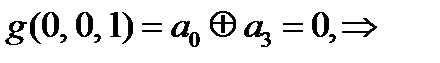
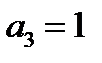
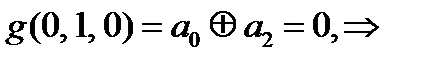
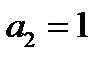
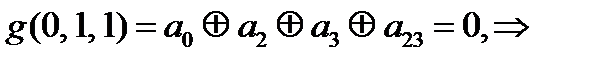
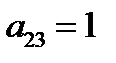
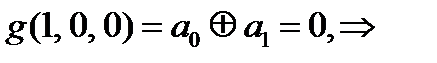
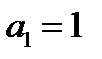
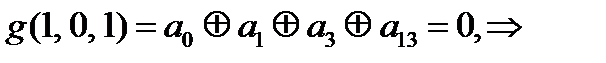
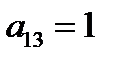
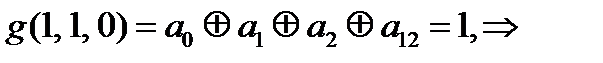
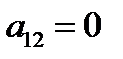
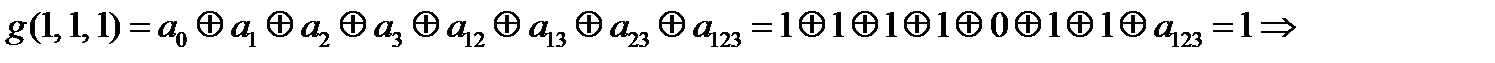
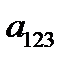 =1
=1
Следовательно, функция 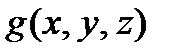 представляется многочленом Жегалкина
представляется многочленом Жегалкина
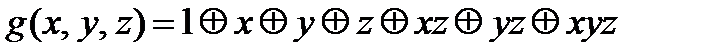
Нелинейная.
Итак, 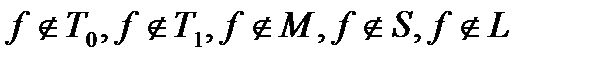 ,
, 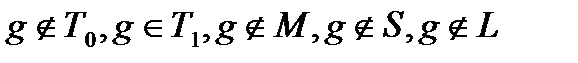
2.3.2. Функция f(x,y,z) представляет из себя функционально полный класс, выразим из неё с помощью суперпозиций константы 0,1, отрицание и конъюнкцию xy.
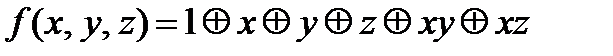
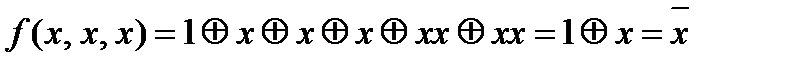
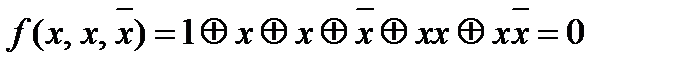
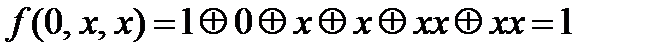
2.3.3. Функция g(x,y,z) представляет из себя функционально полный в слабом смысле класс, выразим из неё с помощью суперпозиций и фиксирования переменных отрицание и конъюнкцию ху.
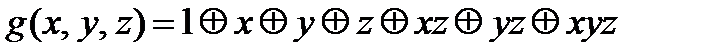
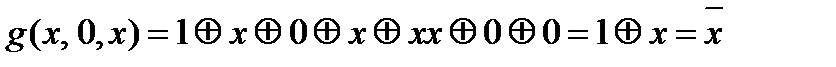
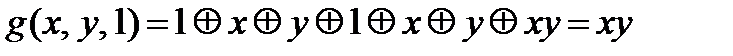
2.3.4. Полученные результаты проверим с помощью построения таблиц.
| x | y | z | f | g | 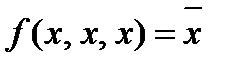
| 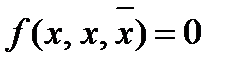
| 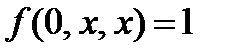
| 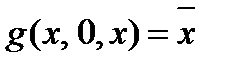
| 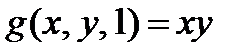
|
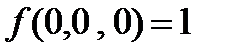
| 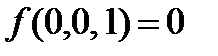
| 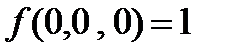
| 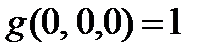
| 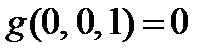
| |||||
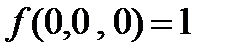
| 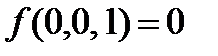
| 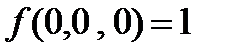
| 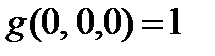
| 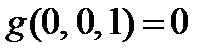
| |||||
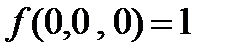
| 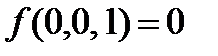
| 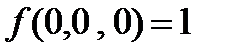
| 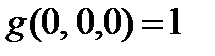
| 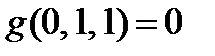
| |||||
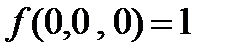
| 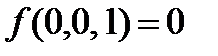
| 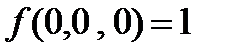
| 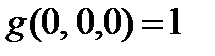
| 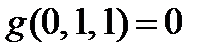
| |||||
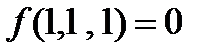
| 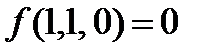
| 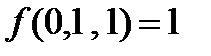
| 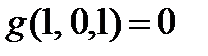
| 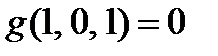
| |||||
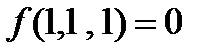
| 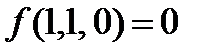
| 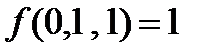
| 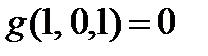
| 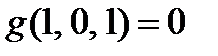
| |||||
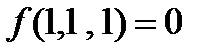
| 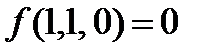
| 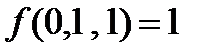
| 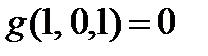
| 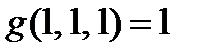
| |||||
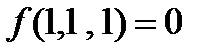
| 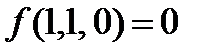
| 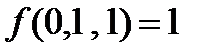
| 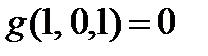
| 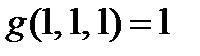
|
 2015-06-28
2015-06-28 623
623







