Задание 2.1

2.1.1. Доопределить функции f(x,y,z), g(x,y,z), h(x,y,z) так, чтобы .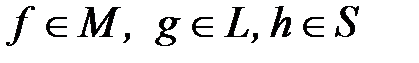

Если построение какой-либо функции невозможно, докажите это.

Выясните вопрос о принадлежности построенных функций к классам 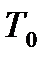и .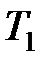

f	g	h
(0 - - 0 1 - - -)	(- - 0 0 1 - 0 -)	(- - 1 0 - - 0 0)

Доопределим функции f(x,y,z), g(x,y,z), h(x,y,z) так чтобы f(x,y,z), была монотонная, g(x,y,z)- линейная, а h(x,y,z) - самодвойственная.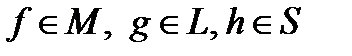

Составим таблицу состояний

f =(0000 1111) монотонна
x	y	z	f	g	h

Функция 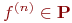называется линейной, если она может быть задана линейным многочленом Жегалкина вида 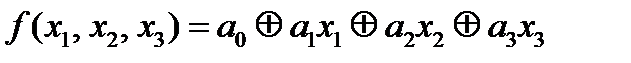где 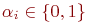при i=0, 1, 2,..., n.

Выпишем, что нам известно про коэффициенты

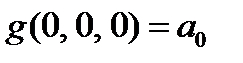
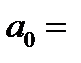
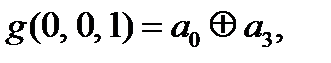
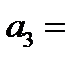
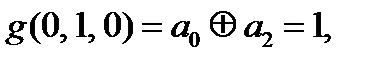
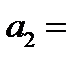
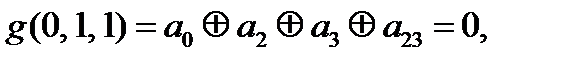
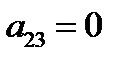
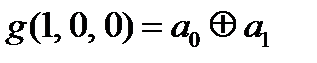
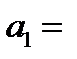
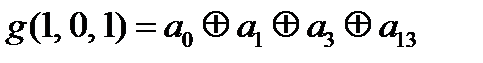
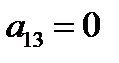
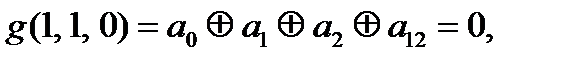
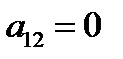
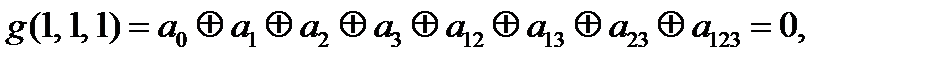
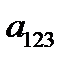=0

Итого 4 условия:

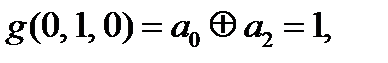
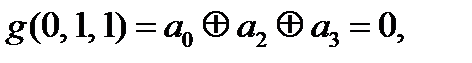
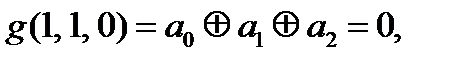
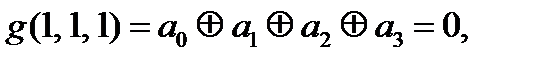
С учетом условия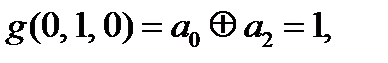

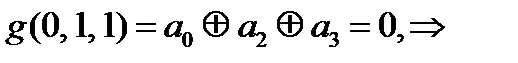
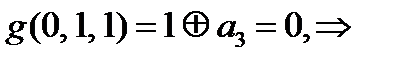
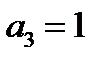
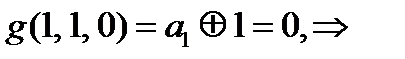
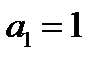
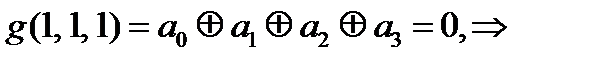
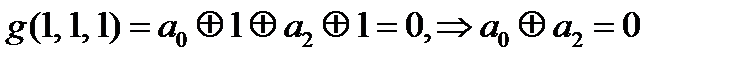
Получили противоречие 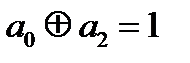и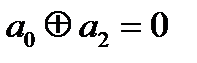

Вывод: g(x,y,z) невозможно доопределить, так чтобы она была линейной.

Функция 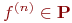называется самодвойственной, если для любого набора аргументов 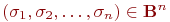имеет место равенство:

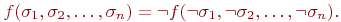
Таким образом, самодвойственные функции принимают на противоположных наборах противоположные значения.

Доопределим h= (11 1 0 1 0 0 0) –самодвойственная.

Задание 2.2.

2.2.1. Можно ли из функции f(x,y,z) с помощью суперпозиций получить g(x,y,z)?

f	g
1000 0000	1100 0011

x	y	z	f	g

Из таблицы, очевидно, что 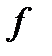не сохраняет 0 и 1, не монотонная, и не самодвойственная.

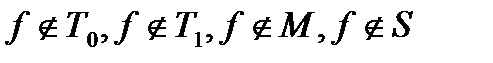
Составим многочлен Жегалкина

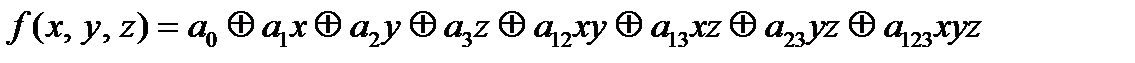
Последовательно подставляя значения переменных и f из таблицы, получаем:

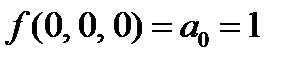
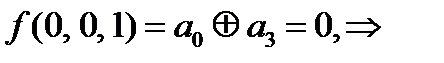
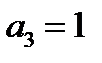
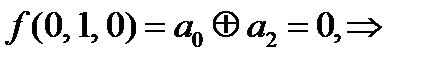
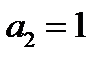
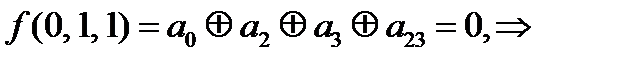
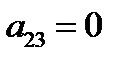
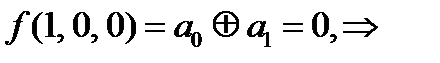
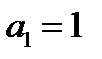
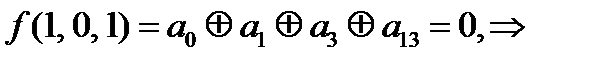
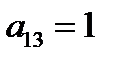дальше можно не считать, функция не линейна, но досчитаем.

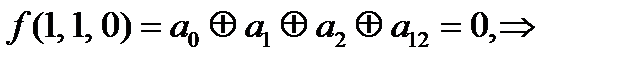
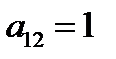
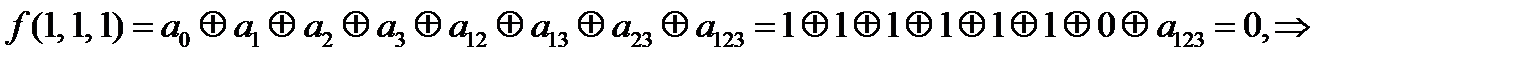
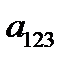=0

Следовательно, функция 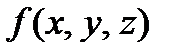представляется многочленом Жегалкина

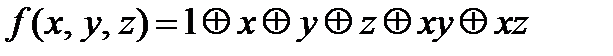
Итак,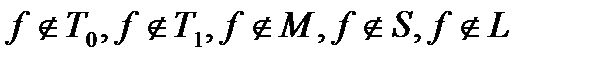

По теореме Поста, замыканием 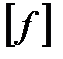будет множество всех булевых функций.

То есть из f при помощи суперпозиции можно получить любую булеву функцию.