1.1 Основные определения
Все данные в MATLAB, например переменные, векторы, матрицы, которые являются по своей сути математическими объектами, представляются в виде массивов. Массив – упорядоченная, пронумерованная совокупность однородных данных. У массива должно быть имя. Массивы различаются по числу размерностей или измерений: однородные, двумерные, многомерные. Размером массива называют число элементов вдоль каждого из измерений. Элементы доступны через индексы. Нумерация элементов массивов в MATLAB начинается с единицы.
Вектор может быть записан в столбик и в строку. Векторы и матрицы обозначаются курсивом, а соответствующие им массивы прямым шрифтом.
1.2 Ввод, сложение и вычитание векторов
Требуется сложить два вектора:
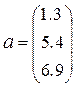 и
и 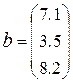 .
.
Для хранения векторов используются массивы a и b, которые вводятся в командной строке с использованием квадратных скобок и с разделением элементов векторов точкой с запятой:
>> a = [1.3; 5.4; 6.9]
a =
1.3000
5.4000
6.9000
>> b = [7.1; 3.5; 8.2];
Для нахождения суммы векторов используется знак плюс:
>> c = a + b
c =
8.4000
8.9000
15.1000
Согласно информации в окне Workspace векторы a, b, c хранятся в двумерных массивах. В столбце Size указано 3х1, т.е. массивы имеют по три строки и одному столбцу, каждый из них занимает 24 байта памяти. Аналогичные сведения можно получить при помощи встроенных функций ndims и size:
>> na = ndims(a)
na =
>> sa = size(a)
sa =
3 1
Матричное представление данных позволяет вычислять значения тригонометрических функций по отношению ко всем элементам вектора:
>> d = sin(c)
d =
0.8546
0.5010
0.5712
Таким образом, если аргумент функции является массивом, то результат функции будет массивом того же размера, но с элементами, равными значению функции от соответствующих элементов исходного массива. Например, извлечение квадратного корня из элементов вектора d со знаком минус:
>> sqrt(-d)
ans =
0 + 0.9244i
0 + 0.7078i
0 + 0.7558i
Вектор-строка вводится в квадратных скобках, однако в отличие от вектора-столбца элементы следует разделять пробелами или запятыми. Операции выполняются аналогично, в результате чего формируется вектор-строка. Например:
>> s1 = [3 4 9 2]
s1 =
3 4 9 2
>> s2 = [5 3 3 2]
s2 =
5 3 3 2
>> s3 = s1 + s2
s3 =
8 7 12 4
>> s4 = log(s3)
s4 =
2.0794 1.9459 2.4849 1.3863
Информация о массивах, в которых хранятся вектор-строки, появляется в окне Workspace. Для определения длины вектор-столбцов или вектор-строк используется встроенная функция length:
>> L = length(s1)
L =
По умолчанию все элементы массивов хранятся с двойной точностью (double) и занимают 8 байтов. Возможно хранение элементов массивов в других форматах: single – для вещественных чисел, требующих для размещения 4 байта, int8, int16, int32 – для целых чисел, занимающих 1, 2 или 4 байта соответственно. Для изменения формата представления предназначены одноименные с типом (Class) функции:
>> q4 = single(s4);
>> q3 = int32(s3);
>> q2 = int16(s2);
>> q1 = int8(s1);
При преобразовании целого числа в случае, когда для его точного представления не хватает отводимой памяти, получается максимальное число для данного типа без предупреждения об ошибке. Поэтому применение целых чисел ограничено. Попытка выполнения арифметических операций над целыми числами разных типов также приводит к ошибке.
1.3 Сцепление и редактирование векторов
Из нескольких вектор-столбцов можно составить один, используя квадратные скобки и разделяя исходные вектор-столбцы точкой с запятой:
>> v1 = [1; 2];
>> v2 = [3; 4; 5];
>> v = [v1; v2]
v =
Для сцепления вектор-строк также применяются квадратные скобки, но сцепляемые вектор-строки отделяются пробелами или запятыми:
>> v1 = [pi pi/2];
>> v2 = [pi/3 pi/4 pi/5];
>> v = [v1 v2]
v =
3.1416 1.5708 1.0472 0.7854 0.6283
Для просмотра и изменения значений элементов массивов удобно использовать редактор массивов Array Editor. Окно редактора открывается после двойного щелчка "мышью" по имени массива v в окне Workspace или нажатию кнопки Open Selection на панели инструментов окна Workspace при положении курсора на имени массива. Переход в редактирование ячейки - по нажатию кнопки F2. Редактировать массив можно с помощью опций контекстного меню и панели инструментов. Следует отметить, что операция Cut приводит только к обнулению элемента массива, а его удаление следует делать по Delete.
Для работы с данными редактор массивов MATLAB предоставляет возможности, аналогичные MS Excel.
Редактор массивов позволяет просматривать значения элементов нескольких массивов. Для этого двойным щелчком вызывается очередной массив и с помощью панели инструментов устанавливается вариант просмотра.
1.4 Обращение к элементам вектора
Для доступа к элементам вектора используется индекс, заключаемый в круглые скобки после имени массива, в котором хранится вектор. Например, для доступа к четвертому элементу массива v, определенного вектор-строкой
>> v = [1.3 3.6 7.4 8.2 0.9];
используется индексация:
>> h = v(4)
h =
8.2000
Указание элемента массива в левой части оператора присваивания приводит к изменению в массиве:
>> v(2) = 555
v =
1.3000 555.0000 7.4000 8.2000 0.9000
Из элементов массива можно формировать новые массивы, например:
>> u = [v(3); v(2); v(1)]
u =
7.4000
555.0000
1.3000
Для помещения определенных элементов вектора в другой вектор в заданном порядке служит индексация при помощи вектора. Например, запись в вектор-строку w четвертого, второго и пятого элементов v производится следующим образом:
>> ind = [4 2 5];
>> w = v(ind)
w =
8.2000 555.0000 0.9000
Для обращения к блокам последовательно расположенных элементов вектора служит индексация при помощи знака двоеточия. Например, для замены нулями элементов со второго по шестой в вектор-строке w из семи элементов требуется выполнить:
>> w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8];
>> w(2:6) = 0;
>> w
w =
0.1000 0 0 0 0 0 9.8000
Индексация при помощи двоеточия используется и при выделении части из большого объема в новый массив:
>> w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8];
>> w1 = w(3:5)
w1 =
3.3000 5.1000 2.6000
Следующий пример показывает формирование вектора-строки w2, содержащего элементы w, кроме четвертого:
>> w2 = [w(1:3) w(5:7)]
w2 =
0.1000 2.9000 3.3000 2.6000 7.1000 9.8000
Для получения аналогичного результата вместо w(5:7) можно написать w(5:end).
Элементы массива могут входить в выражения. Вычисление, например, среднего геометрического из элементов вектора u можно сделать следующим образом:
>> gm = (u(1) * u(2) * u(3)) ^ (1/3)
gm =
17.4779
1.5 Применение функций обработки данных
Элементы вектора перемножаются при помощи функции prod:
>> z = [3; 2; 1; 4; 6; 5];
>> p = prod(z)
p =
Следовательно, найти среднее геометрическое можно так:
>> gm = prod(z) ^ (1/length(z))
gm =
2.9938
Функция sum предназначена для суммирования элементов вектора.
Для вычисления среднего арифметического – функция mean:
>> mean(z)
ans =
3.5000
Для нахождения минимума и максимума из элементов вектора – функции min и max:
>> M = max(z)
M =
>> m = min(z)
m =
При обращении к функции min с двумя векторами в качестве входных аргументов получится вектор, каждый элемент которого есть минимум из двух элементов исходных векторов с одинаковыми размерами:
>> p = [3 12 8];
>> s = [4 10 7];
>> min (p, s)
ans =
3 10 7
Следующая команда позволяет определить индекс минимального элемента массива, который будет занесен в переменную k:
>> [m, k] = min(z)
m =
k =
Для поиска индексов элементов, удовлетворяющих определенному условию, служит функция find. Например, требуется найти номера всех элементов вектора x, равных максимальному значению (знак == обозначает логическое равенство):
>> x = [1 2 5 3 4 5 1 5];
km = find(x == max(x))
km = 3 6 8
К числу основных функций для работы с векторами относится функция sort упорядочения вектора по возрастанию его элементов:
>> r = [9.4 -2.3 -5.2 7.1 0.8 1.3];
>> R = sort (r)
R =
-5.2000 -2.3000 0.8000 1.3000 7.1000 9.4000
Эту функцию можно использовать для упорядочения вектора по убыванию:
>> R1 = -sort (-r)
R1 =
9.4000 7.1000 1.3000 0.8000 -2.3000 -5.2000
Упорядочить элементы вектора в порядке возрастания их модулей можно с помощью функции abs:
>> R2 = sort (abs(r))
R2 =
0.8000 1.3000 2.3000 5.2000 7.1000 9.4000
Вызов sort с двумя выходными аргументами приводит к образованию массива индексов соответствия элементов упорядоченного и исходного массивов:
>> [rs, ind] = sort(r)
rs =
-5.2000 -2.3000 0.8000 1.3000 7.1000 9.4000
ind =
3 2 5 6 4 1
Равенство r(ind(k)) = rs(k) для k от 1 до length(k) связывает исходный массив r, упорядоченный rs и массив индексов ind.
Если аргументом функций max и min является вектор, состоящий из комплексных чисел, то результатом является максимальный и минимальный по модулю элемент. Функция sort также упорядочивает комплексный вектор по модулю, а компоненты с равными модулями располагаются в порядке возрастания фаз.
Информацию о функциях обработки данных можно узнать по команде help datafun.
1.6 Поэлементные операции с векторами
Для поэлементного умножения векторов равной длины используется операция.* (точка и звездочка, записанные без пробелов). Например:
>> v1 = [2 -3 4 1];
>> v2 = [7 5 -6 9];
u = v1.* v2
u =
14 -15 -24 9
Операция.^ - поэлементное возведение в степень:
>> p = v1.^ 2
p =
4 9 16 1
Показателем степени может быть вектор той же длины, что и возводимый в степень. При этом каждый элемент первого вектора возводится в степень, равную соответствующему элементу второго вектора:
>> P = v1.^ v2
P =
128.0000 -243.0000 0.0002 1.0000
Деление – операция./
>> d = v1./ v2
d =
0.2857 -0.6000 -0.6667 0.1111
Обратное поэлементное деление (деление элементов второго вектора на соответствующие элементы первого) - операция.\
>> dinv = v1.\ v2
dinv =
3.5000 -1.6667 -1.5000 9.0000
Таким образом, точка в MATLAB используется не только для ввода десятичных дробей, но и для указания поэлементных операций для массивов одинакового размера.
К поэлементным относятся операции вектора с числом. Сложение вектора и числа не приводит к сообщению об ошибке. MATLAB прибавляет число к каждому элементу вектора (это справедливо и для вычитания):
>> v = [4 6 8 10];
>> s = v + 1.2
s =
5.2000 7.2000 9.2000 11.2000
>> s1 = 1.2 + v
s1 =
5.2000 7.2000 9.2000 11.2000
>> r = 1.2 – v
r =
-2.8000 -4.8000 -6.8000 -8.8000
>> r1 = v – 1.2
r1 =
2.8000 4.8000 6.8000 8.8000
Умножать вектор на число можно как справа, так и слева:
>> v = [4 6 8 10];
>> p = v*2
p =
8 12 16 20
>> p1 = 2*v
p1 =
8 12 16 20
Делить при помощи операции / можно вектор на число:
>> p = v/2
p =
2 3 4 5
Попытка деления числа на вектор-строку (>> p = 2/v) приводит к ошибке. Но при делении числа на вектор-столбец сообщение об ошибке не выдается, т.к. происходит решение системы линейных уравнений с прямоугольной матрицей, в которой число неизвестных превосходит число уравнений.
Для деления числа на каждый элемент вектора с записью результата в новый вектор следует использовать операцию./
>> w = [4 2 6];
>> d = 12./w
d =
3 6 2
Все указанные операции применимы как к векторам-строкам, так и к векторам-столбцам.
Для вектора-столбца u, к примеру с тремя комплексными переменными (в частности с вещественными), сопряженный к нему u* определяется как вектор-строка из его комплексно-сопряженных элементов, а транспонированный uT – просто как вектор-строка из его элементов, например:
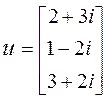 , u* = [2-3i 1+2i 3-2i], uT = [2+3i 1-2i 3+2i].
, u* = [2-3i 1+2i 3-2i], uT = [2+3i 1-2i 3+2i].
Аналогично определяется сопряжение и транспонирование для вектора-строки, приводящее к вектору-столбцу. Ясно, что для векторов, состоящих только из действительных чисел, операции сопряжения и транспонирования совпадают.
Для нахождения сопряженного вектора используется апостроф, а для транспонирования следует применять точку с апострофом:
>> u = [2 + 3i; 1 - 2i; 3 + 2i];
>> v = u'
v =
2.0000 - 3.0000i 1.0000 + 2.0000i 3.0000 - 2.0000i
>> v = u.'
v =
2.0000 + 3.0000i 1.0000 - 2.0000i 3.0000 + 2.0000i
Операции.' и ' над вещественными векторами приведут к одинаковым результатам.
1.7 Скалярное произведение векторов
Скалярное произведение (его иногда называют внутренним) векторов a и b длины N, состоящих из действительных чисел, определяется формулой 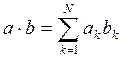 . Следовательно, для вычисления скалярного произведения необходимо просуммировать компоненты вектора, полученного в результате поэлементного умножения a на b, т.е. надо использовать функцию sum и поэлементное умножение. Например для скалярного умножения векторов
. Следовательно, для вычисления скалярного произведения необходимо просуммировать компоненты вектора, полученного в результате поэлементного умножения a на b, т.е. надо использовать функцию sum и поэлементное умножение. Например для скалярного умножения векторов
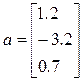 и
и 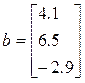 требуется следующая последовательность команд:
требуется следующая последовательность команд:
>> a = [1.2; -3.2; 0.7];
>> b = [4.1; 6.5; -2.9];
>> s = sum(a.* b)
s =
-17.9100
Скалярное произведение векторов можно вычислить по функции dot:
>> s = dot(a, b);
Функция dot позволяет найти длину (т.е. модуль) вектора a 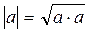 :
:
>> d = sqrt(dot(a, a))
d =
3.4886
1.8 Векторное произведение векторов
Векторное произведение a x b определено только для трехмерного пространства, т.е. для векторов, состоящих из трех элементов. Результатом также является вектор из трехмерного пространства. Для вычисления векторного произведения в MATLAB служит функция cross:
>> a = [1.2; -3.2; 0.7];
>> b = [4.1; 6.5; -2.9];
>> c = cross(a, b)
c =
4.7300
6.3500
20.9200
Смешанное произведение векторов a, b, c определяется по формуле abc=a.(bxc). Модуль смешанного произведения равен объему параллелепипеда, построенного на этих векторах. При 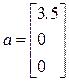
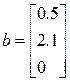
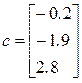
>> a = [3.5; 0; 0];
>> b = [0.5; 2.1; 0];
>> c = [-0.2; -1.9; 2.8];
>> V = abs(dot(a, cross(b, c)))
V =
20.5800
1.9 Внешнее произведение векторов
Внешним произведением векторов  ,
,  называется матрица
называется матрица 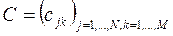 размера NxM, элементы которой вычисляются по формуле
размера NxM, элементы которой вычисляются по формуле 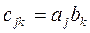 . Вектор-столбец a в MATLAB представляется в виде двумерного массива размера N на один. Вектор-столбец b при транспонировании переходит в вектор-строку размера один на M. Вектор-строка и вектор-столбец есть матрицы, у которых один из размеров равен единице. Фактически
. Вектор-столбец a в MATLAB представляется в виде двумерного массива размера N на один. Вектор-столбец b при транспонировании переходит в вектор-строку размера один на M. Вектор-строка и вектор-столбец есть матрицы, у которых один из размеров равен единице. Фактически 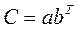 , где умножение происходит по правилу матричного произведения (оператор "звездочка"):
, где умножение происходит по правилу матричного произведения (оператор "звездочка"):
>> a = [1; 2; 3];
>> b = [5; 6; 7];
>> C = a*b'
C =
5 6 7
10 12 14
15 18 21
Таким образом, в командное окно выведена матрица в привычном виде – по строкам. Для просмотра переменных рабочей среды можно использовать окно Workspace или команду whos. Числа, векторы, матрицы хранятся в двумерных массивах. Числа – в массивах, размерностью один на один, вектор-столбцы и вектор-строки – в массивах, у которых одно из измерений равно единице, а для матриц выделяются двумерные массивы подходящих размеров.
1.10 Отображение функции в виде таблицы
При сравнительно небольшом количестве значений удобно отображать функцию в виде таблицы. Например, требуется вывести в командное окно таблицу значений функции: 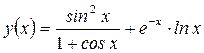 в точках 0.2, 0.3, 0.5, 0.8, 1.3, 1.7, 2.5. Для этого создается вектор-строка x, содержащий координаты заданных точек. Затем вычисляется функция y(x) от каждого элемента вектора x и полученные значения записываются в вектор-строку y.
в точках 0.2, 0.3, 0.5, 0.8, 1.3, 1.7, 2.5. Для этого создается вектор-строка x, содержащий координаты заданных точек. Затем вычисляется функция y(x) от каждого элемента вектора x и полученные значения записываются в вектор-строку y.
>> x = [0.2 0.3 0.5 0.8 1.3 1.7 2.5]
>> x =
0.2000 0.3000 0.5000 0.8000 1.3000 1.7000 2.5000
>> y = sin(x).^2./ (1 + cos(x)) +exp(-x).* log(x)
y =
-1.2978 -0.8473 -0.2980 0.2030 0.8040 1.2258 1.8764
Таблице можно придать более удобный для чтения вид, расположив значения функции непосредственно под значениями аргумента:
>> x
x =
0.2000 0.3000 0.5000 0.8000 1.3000 1.7000 2.5000
>> y
y =
-1.2978 -0.8473 -0.2980 0.2030 0.8040 1.2258 1.8764
Часто требуется вывести значение функции в точках отрезка, отстоящих друг от друга на равное расстояние, т.е. шаг. Для ввода таких векторов используется двоеточие. Например, если шаг равен 0.2:
>> x = 1: 0.2: 2
x =
1.0000 1.2000 1.4000 1.6000 1.8000 2.0000
Причем необязательно надо заботиться о том, чтобы сумма предпоследнего значения и шага равнялась бы конечному значению, т.к. вектор-строка заполнится до элемента, не превосходящего указанное конечное значение.
Шаг может быть и отрицательным:
>> x = 1.9: -0.2: 1
x =
1.9000 1.7000 1.5000 1.3000 1.1000
В случае отрицательного шага начальное значение должно быть больше или равно конечному для получения непустого вектора-строки.
Для заполнения вектора-столбца элементами, например, начинающимися с нуля и заканчивающимися 0.5 с шагом 0.1, следует заполнить вектор-строку, а затем использовать операцию транспонирования:
>> x =(0: 0.1: 0.5)'
x =
0.1000
0.2000
0.3000
0.4000
0.5000
Элементы вектора, заполняемого при помощи двоеточия, могут быть только вещественные, поэтому для транспонирования можно набрать знак апострофа вместо точки с апострофом.
Шаг, равный единице, допускается не указывать при автоматическом заполнении:
>> x = 1: 5
x =
1 2 3 4 5
Если результирующие векторы не помещаются на экране целиком, то они выводятся по частям. Например, требуется вычислить значения функции 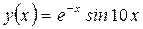 на отрезке [0, 1] с шагом 0.05:
на отрезке [0, 1] с шагом 0.05:
>> x = 0: 0.05:1;
>> y = exp(-x).* sin(10*x);
Результат, выведенный на экран, не похож на таблицу:
>> x
x =
Columns 1 through 8
0 0.0500 0.1000 0.1500 0.2000 0.2500 0.3000 0.3500
Columns 9 through 16
0.4000 0.4500 0.5000 0.5500 0.6000 0.6500 0.7000 0.7500
Columns 17 through 21
0.8000 0.8500 0.9000 0.9500 1.0000
>>y
y =
Columns 1 through 8
0 0.4560 0.7614 0.8586 0.7445 0.4661 0.1045 -0.2472
Columns 9 through 16
-0.5073 -0.6233 -0.5816 -0.4071 -0.1533 0.1123 0.3262 0.4431
Columns 17 through 21
0.4445 0.3413 0.1676 -0.0291 -0.2001
Так как x и y хранятся в двумерных массивах один на двадцать один, то они выводятся по столбцам, каждый из которых состоит из одного элемента. Количество элементов, выводимых в одну строку, определяется текущими размерами окна и форматом вывода данных.
Одним из способов получения таблицы является формирование матрицы из двух столбцов, первый - значения абсцисс, а второй – ординат:
>> [x' y']
ans =
0 0
0.0500 0.4560
0.1000 0.7614
0.1500 0.8586
......
0.9500 -0.0291
1.0000 -0.2001
Часто более удобным оказывается графическое представление функций.
1.11 Графики функций одной переменной в линейном масштабе
MATLAB позволяет строить графики функций в линейном, логарифмическом и полулогарифмическом масштабах. Причем в одном окне можно построить графики нескольких функций.
Основным средством двумерной графики в линейном масштабе является функция plot. Типичный вариант ее использования выглядит так:
plot(x, y)
Здесь x и y - векторы одинаковой длины, задающие координаты точек, выводимых на график. Таким образом, для построения графика функции в рабочей среде MATLAB должны быть определены два вектора одинаковой размерности. Вектор x содержит значения аргументов, а y - значения функции от этих аргументов. По умолчанию точки с координатами (x(i), y(i)) соединяются прямыми линиями синего цвета. При этом оси автоматически масштабируются для оптимального расположения графика в окне.
На рис.1 показан пример графика функции 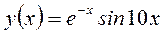 , определенной на отрезке [0, 1]. Набор команд выглядит следующим образом:
, определенной на отрезке [0, 1]. Набор команд выглядит следующим образом:
>> x = 0: 0.05: 1;
>> y = exp(-x).*sin(10*x);
>> plot(x, y)
После выполнения команд появляется окно с графиком функции (рис.1).
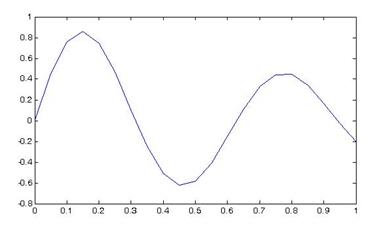
Рис. 1 Пример графика функции
Для построения графиков удобно расположить на экране командное окно MATLAB и окно с графиком так, чтобы они не перекрывались. Например, используя кнопку Dock Figure (справа в строке меню окна), можно встроить графическое окно в рабочую среду. Для получения отдельного графического окна следует нажать на кнопку Undock Figure.
Построенный график функции не должен иметь изломов, т.к. сама функция гладкая. Для точного построения графика необходимо вычислить функцию в большом числе точек на отрезке [0, 1], т.е. задать меньший шаг при вводе вектора x. Следующие команды:
>> x = 0: 0.01: 1;
>> y = exp(-x).*sin(10*x);
>> plot(x, y)
приводят к построению графика функции в виде плавной кривой (рис.2).
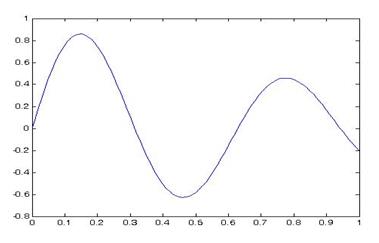
Рис. 2 Пример сглаженного графика функции
Для сравнения нескольких функций их графики отображаются на одних осях. Например, на рис.3 показаны графики функций 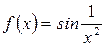 ,
, 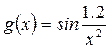 на отрезке [-1, -0.3].
на отрезке [-1, -0.3].
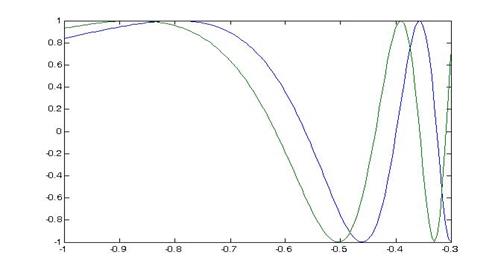
Рис. 3 Пример двух графиков на одних осях
Графики получены при помощи следующей последовательности команд:
>> x = -1: 0.005: -0.3;
>> f = sin(x.^-2);
>> g = sin(1.2*x.^-2);
>> plot(x, f, x, g)
Если функции определены на разных отрезках, то при построении графиков MATLAB выбирает максимальный отрезок, содержащий остальные. Важно только в каждой паре векторов абсцисс и ординат, количество которых может быть произвольным, указать в plot соответствующие друг другу векторы.
Если значения функций сильно отличаются друг от друга, то график функции с небольшими значениями может сливаться с осью абсцисс. Для устранения этого эффекта используется функция plotyy, которая выводит графики в окно с двумя вертикальными осями, имеющими подходящий масштаб. Например, на рис.4 показаны графики двух функций 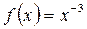 и
и 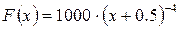 .
.
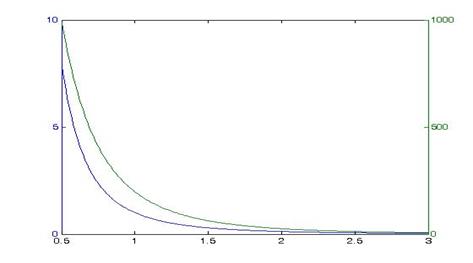
Рис. 4 Пример сравнения функций при помощи plotyy
Графики получены при помощи следующей последовательности команд:
>> x = 0.5: 0.01: 3;
>> f = x.^-3;
>> F = 1000*(x+0.5).^-4;
>> plotyy(x, f, x, F)
Цвет графика совпадает с цветом соответствующей ему оси ординат.
Функцию plot допустимо использовать с одним аргументом, что приводит к построению "графика вектора", т.е. зависимости значений элементов вектора от их номеров.
1.12 Графики функций одной переменной в логарифмическом масштабе
Для построения графиков в логарифмическом и полулогарифмическом масштабах служат функции:
· loglog – логарифмический масштаб по обеим осям,
· semilogx – логарифмический масштаб только по оси абсцисс,
· semilogy – логарифмический масштаб только по оси ординат.
Аргументы этих функций задаются в виде пары векторов значений абсцисс и ординат аналогично функции plot. На рис.5 показаны графики функций 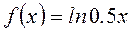 и
и 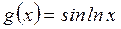 на отрезке [0.1, 5] в логарифмическом масштабе по оси x.
на отрезке [0.1, 5] в логарифмическом масштабе по оси x.
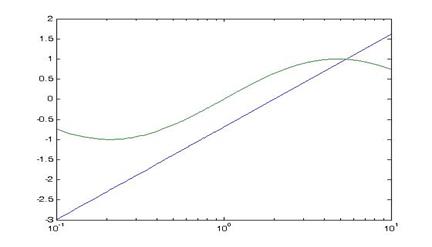
Рис. 5 Графики в полулогарифмической шкале
Графики получены при помощи последовательности команд:
>> x = 0.1: 0.01: 10;
>> f = log(0.5*x);
>> g = sin(log(x));
>> semilogx (x, f, x, g)
Функции loglog и semilogy вызываются аналогичным образом.
 2015-06-28
2015-06-28 548
548







