ВВЕДЕНИЕ
По дисциплине "Теория вероятностей и математическая статистика" выполняется одна контрольная работа. Выбор варианта осуществляется по двум последним цифрам номера зачетной книжки.
Таблица
Варианты контрольных заданий
| № варианта | №№ задач | ||||||
К сдаче экзамена или зачета допускаются студенты, имеющие на руках зачтенные контрольные работы.
ПЕРЕЙТИ К ЗАДАЧАМ
РАБОЧАЯ ПРОГРАММА
СЛУЧАЙНЫЕ СОБЫТИЯ
Основные понятия теории вероятностей. Виды событий. Сумма и произведение случайных событий. Классическое определение вероятности. Статистическая вероятность. Геометрические вероятности.
Теоремы сложения вероятностей для несовместных и совместных событий. Условная вероятность. Теоремы умножения для независимых и зависимых событий.
Формулы полной вероятности и Бейеса.
Повторение испытаний. Формула Бернулли. Локальная и интегральная теоремы Лапласа. Формула Пуассона.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
1. Дискретные случайные величины. Функция распределения случайной величины и ее свойства; числовые характеристики и их свойства; биномиальное распределение.
2. Непрерывные случайные величины. Функция распределения и плотность распределения вероятностей непрерывной случайной величины, их связь и свойства; числовые характеристики; равномерное, нормальное и показательное распределения.
3. Закон больших чисел. Центральная предельная теорема в формулировке Ляпунова.
4. Системы случайных величин: функция распределения и плотность распределения вероятностей, числовые характеристики (включая корреляционный момент и коэффициент корреляции).
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
1. Генеральная и выборочная совокупности. Вариационный ряд. Полигон, гистограмма.
2. Статистическое оценивание параметров распределения по выборке. Состоятельность, эффективность и несмещенность оценки. Выборочное среднее и выборочная дисперсия.
3. Понятие об интервальном оценивании. Доверительный интервал для оценки математического ожидания нормального распределения.
4. Выборочные уравнения прямых линий регрессии.
ЛИТЕРАТУРА
1. Гурский Е.И. Теория вероятностей с элементами математической статистики. М.: Выш. шк., 1971.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Выш. шк., 1977.
3. Мацкевич И.П., Свирид Г.П. Высшая математика. Теория вероятностей и математическая статистика. М.: Выш. шк., 1993.
4. Вентцель Е.С. Теория вероятностей. М.:Наука, 1969.
5. Гурский Е.И. Сборник задач по теории вероятностей и математической статистике. М.: Выш. шк., 1975.
6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Выш. шк., 1975.
7. Мацкевич И.П., Свирид Г.П., Булдык Г.М. Сборник задач и упражнений по высшей математике. Теория вероятностей и математическая статистика. М.: Выш. шк., 1996.
8. Рябушко А.П. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. М.: Выш. шк., 1992.
СЛУЧАЙНЫЕ СОБЫТИЯ
В теории вероятностей событием называется всякое явление, которое может произойти или не произойти в результате опыта. Достоверное событие - это событие, которое обязательно произойдет в результате опыта. Невозможное событие - это событие, которое заведомо не произойдет в результате опыта. Случайное событие - это событие, которое может произойти или не произойти в результате опыта. Например, при подбрасывании монеты выпадение герба (событие А) или цифры (событие В) - случайные события.
События называются несовместными, если появление одного из них исключает появление другого. В противном случае два события называются совместными. События А1, А2 ,..., Аn называются несовместными, если все они попарно несовместны.
Группа несовместных событий называется полной, если в результате опыта обязательно наступит одно из событий этой группы.
Противоположными называются два несовместных события, образующих полную группу.Например, если событие А - попадание в цель, то промах - противоположное событие 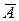 (читается: не А).
(читается: не А).
Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого события, и зависимыми в противном случае.
Суммой А+В событий А и В называют событие, состоящее в появлении одного из них или обоих вместе. Если события А и В - несовместные события, то А+В означает появление одного из них. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Произведением называется событие, состоящее в совместном появлении всех этих событий.
Решение многих задач на расчет вероятностей случайных событий целесообразно проводить по следующей схеме:
1. Ввести обозначение событий, вероятности которых известны или легко рассчитываются исходя из условия задачи, а также событий, вероятность которых необходимо найти ("неизвестные" события).
2. С помощью действий сложения и умножения событий "неизвестные" события выразить через "известные".
3. Перейти к вероятностям событий, используя приведенные ниже формулировки теорем сложения и умножения вероятностей.
Теорема 1. Сложение вероятностей несовместных событий. Вероятность появления одного из нескольких несовместных событий равна сумме вероятностей этих событий.
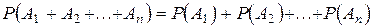 . (1)
. (1)
Типичной ошибкой является применение формулы (1) для совместных событий. Более общей является теорема сложения вероятностей совместных событий.
Теорема 2. Вероятность появления хотя бы одного из двух событий равна сумме вероятностей этих событий без вероятности их совместного появления.
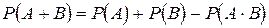 . (2)
. (2)
Замечание: для определения вероятности суммы трех и более совместных событий целесообразно перейти к противоположному событию, так как в этом случае формула (2) неприменима.
Теорема 3. У множение вероятностей независимых событий.
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
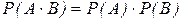 . (3)
. (3)
Теорема 4. Умножение вероятностей зависимых событий.
Вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого, вычисленную при условии, что первое событие имело место.
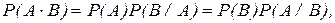 (4)
(4)
где 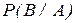 - условная вероятность события
- условная вероятность события 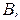 вычисленная при условии, что событие
вычисленная при условии, что событие 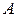 уже произошло.
уже произошло.
Пример 1. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором два вопроса.
Решение.
Воспользуемся приведенной выше схемой решения таких задач.
1.Введем обозначение событий: событие А 1 - студент знает первый вопрос, событие А 2 - второй, событие В - оба вопроса.
2.Чтобы произошло событие В, необходимо наступление и события А 1, и события А 2, т.е., 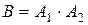 .
.
3.События А 1 и А 2 - зависимые, так как вероятность события А 2 зависит от того, наступило или нет событие А 1. Действительно, 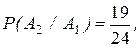 а
а 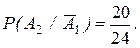 Поэтому при переходе к вероятностям применим формулу (4)
Поэтому при переходе к вероятностям применим формулу (4)
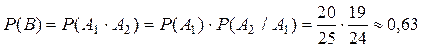 .
.
Пример 2. Три станции независимо друг от друга передают по одному сообщению. Вероятности приема этих сообщений четвертой станцией равны соответственно 0,7; 0,8; 0,9. Найти вероятность того, что а) будет принято хотя бы одно сообщение; б) будет принято одно сообщение.
Решение.
1. Пусть событие Аi - принято сообщение i -ой станции (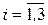 ). Вероятности этих событий известны и равны Р (А1)=0,7, Р (А2)=0,8, Р (А3)=0,9. "Неизвестные" события - В 1 (принято хотя одно сообщение) и В 2 (только одно).
). Вероятности этих событий известны и равны Р (А1)=0,7, Р (А2)=0,8, Р (А3)=0,9. "Неизвестные" события - В 1 (принято хотя одно сообщение) и В 2 (только одно).
2а. Событие В 1 означает наступление хотя бы одного из событий Аi (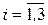 ), то есть представляет собой сумму этих событий
), то есть представляет собой сумму этих событий
В 1 = А 1 +А 2 +А 3 .
Однако, события А1, А2, А3 - совместные. Поэтому перейдем к противоположному событию 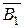 - означающему, что не принято ни одно сообщение, то есть произошли события
- означающему, что не принято ни одно сообщение, то есть произошли события 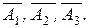 Тогда
Тогда 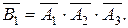
3а Поскольку указанные события независимые, то
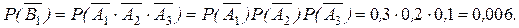
Наконец 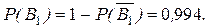
2б. Событие В 2 (принято сообщение только одной станции) означает, что принято сообщение или только первой станции (обозначим это событие через Н1), или только второй станции (Н2), или только третьей (Н3), то есть 
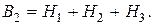
Отметим, что в отличие от предыдущего примера составляющие сумму события Нi (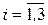 ) - несовместные. Выразим их через события Аi.
) - несовместные. Выразим их через события Аi.
Событие Н1 наступает при появлении трех событий: 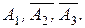

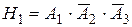 (помимо того, что принято сообщение первой станции (соб. А 1) должны не быть приняты сообщения второй (
(помимо того, что принято сообщение первой станции (соб. А 1) должны не быть приняты сообщения второй (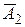 ) и третьей станции (
) и третьей станции (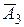 )). Аналогично
)). Аналогично
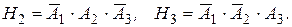
3б.Учитывая независимость событий Аi получим
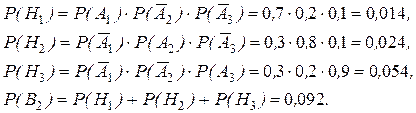
Формула полной вероятности получается как следствие теорем сложения и умножения вероятностей.
Пусть событие А может наступить при условии появления одного из несовместных событий Н 1, Н 2,..., Н n, образующих полную группу.(эти события называют гипотезами). Вероятности этих гипотез известны: Р(Н1), Р(Н2),..., Р(Нn); известны условные вероятности наступления события А при осуществлении каждой из гипотез: P(A/H1), P(A/H2),..., P(A/Hn). Тогда вероятность события А равна сумме парных произведений вероятностей гипотез на вероятности события А при условии, что соответствующая гипотеза осуществилась, то есть
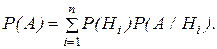 (5)
(5)
Пример 3. Найти вероятность прохождения тока через цепь, если вероятности того, что контакты 1, 2, 3 и 4 замкнуты, равны р1, р 2, р 3, р 4, соответственно. Считать, что контакты действуют независимо друг от друга.
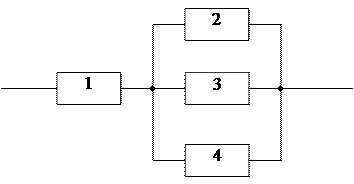

Решение.
Пусть событие С - ток проходит через цепь, событие В - через параллельный участок, событие Аi - замкнут i- ый контакт (i = 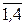 ).
).
Рассмотрим сначала параллельный участок цепи. Через него ток не проходит (событие 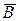 ), если разомкнуты все три контакта (2, 3, 4), т.е.
), если разомкнуты все три контакта (2, 3, 4), т.е.
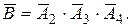
Так как контакты действуют независимо, то
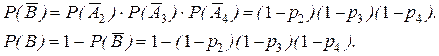
Контакт 1 и параллельный участок соединены последовательно. При таком виде соединения ток должен проходить через оба участка т.е.

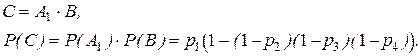
Пример 4. При передаче сообщений в двоичном коде сигналы "0" и "1" встречаются в соотношении 3:2. Определить вероятность того, что сигнал искажен, если из-за помех искажается в среднем 4% сигналов "0" и 2% сигналов "1".
Решение.
Соб. А состоит в том, что принятый сигнал искажен. Пусть Н1 - гипотеза, что передавался сигнал "0"; Н2 - гипотеза, что передавался сигнал "1". Тогда
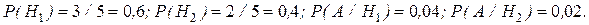
Окончательно по формуле полной вероятности имеем
Р(А)= 0,6.0,04+0,4.0,02=0,032.
Применение теоремы умножения для двух зависимых событий А и В позволяет из формулы (4) найти условную вероятность появления события В в предположении, что произошло событие А
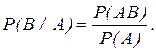 (6)
(6)
С учетом формулы полной вероятности (5) получается формула Бейеса
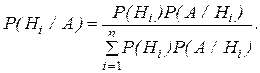 (7)
(7)
Формула Бейеса позволяет определить вероятности гипотез после опыта в предположении, что в результате опыта наступило событие А при известных вероятностях гипотез Hi до опыта.
Отметим, что формулы (6) и (7) применимы, когда в условии примера указан результат опыта. При этом за соб. А принимается событие, которое уже произошло.
Пример 5. В условиях предыдущего примера определить вероятность того, что передавался сигнал "0", если известно, что сигнал искажен.
Решение.
В этом примере необходимо найти условную вероятность P(H1/A), для чего воспользуемся формулой Бейеса
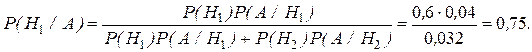
Сравнивая полученный результат с вероятностью гипотезы Н1 до опыта (0,6), видим, что произошла переоценка вероятностей гипотез. Вероятность первой гипотезы увеличилась, а второй - уменьшилась (P(H2 /A) ==1-0,75=0,25).
Пример 6. Три телефониста передают текст. Первый передает 60% текста, второй - 30%, третий - остальную часть текста. Вероятности достоверной передачи текста телефонистами соответственно равны 0,9; 0,8; и 0,6. Определить вероятности того, что текст передавал первый, второй или третий телефонисты при условии, что текст был передан правильно.
Решение.
Событие А состоит в том, что текст передан правильно. Пусть Н1, Н2 и Н3 - гипотезы, состоящие в том, что текст передавали соответственно первый, второй или третий телефонисты. Тогда
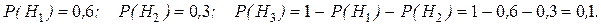
Условные вероятности события А: P(A/H1) =0,9; P(A/H2) =0,8; P(A/H3) =0,6.
По формуле полной вероятности (5) получаем
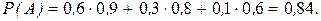
По формуле Бейеса (7) вероятности гипотез после опыта при условии правильной передачи текста равны:
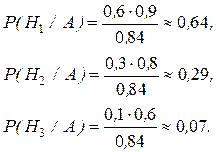
Ряд задач, имеющих практическое применение, связан с неоднократным повторением испытаний в одинаковых условиях. При их решении можно сразу переходить к вероятностям событий, используя для этого подходящую формулу (формулы Бернулли или Пуассона, локальную или интегральную теоремы Лапласа).
Пусть вероятность появления события А в одном испытании равна р(0<p<1) и нам необходимо найти вероятность появления события А ровно m раз в n испытаниях P n (m). Любой из устраивающих нас результатов испытаний можно записать в виде 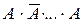 , где событие А встречается m раз, а событие
, где событие А встречается m раз, а событие 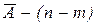 раз. Его вероятность будет по теореме умножения вероятностей независимых событий равна
раз. Его вероятность будет по теореме умножения вероятностей независимых событий равна 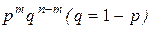 , а количество таких случаев - количеству способов, которыми можно расположить букву А в m местах из n возможных, т.е. числу сочетаний из n элементов по m
, а количество таких случаев - количеству способов, которыми можно расположить букву А в m местах из n возможных, т.е. числу сочетаний из n элементов по m
 .
.
Учитывая несовместность рассматриваемых случаев, получаем формулу Бернулли
Pn(m)=Cnm pm qn-m, (8)
где q=1-p.
При больших n,m в виду громоздкости вычислений вместо формулы Бернулли используют асимптотические формулы, которые позволяют приближенно определить вероятность.
Согласно локальной теоремы Лапласа
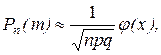 (9)
(9)
где 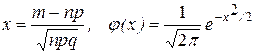 .
.
В большинстве учебников и задачников по теории вероятностей приводятся таблицы значений функции 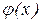 .
.
Если вероятность появления события в одном испытании мала, более точный результат дает формула Пуассона
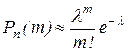 , (10)
, (10)
где 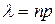 .
.
Наконец в случаях, когда необходимо вычислить вероятность того, что событие А появится в п испытаниях не менее m1 и не более m2 раз 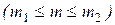 используют интегральную теорему Лапласа
используют интегральную теорему Лапласа
P n 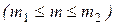
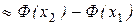 , (11)
, (11)
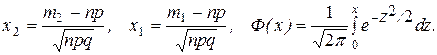
Функция 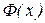 называется функцией Лапласа. Ее значения при изменении аргумента от нуля до пяти приведены в специальных таблицах. Для х >5 можно принять
называется функцией Лапласа. Ее значения при изменении аргумента от нуля до пяти приведены в специальных таблицах. Для х >5 можно принять 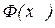 =0,5, а при x <0 используется свойство нечетности функции Лапласа (Ф(-х)=-Ф(х)).
=0,5, а при x <0 используется свойство нечетности функции Лапласа (Ф(-х)=-Ф(х)).
Следует подчеркнуть, что авторы некоторых учебников вводят функцию Лапласа иначе, например как 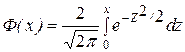 [1].
[1].
Поэтому при использовании соответствующих таблиц выбранное значение Ф(х) необходимо уменьшить в 2 раза.
Пример 7. Вероятность потери каждого вызова при наборе телефонного номера равна 0,1. Найти вероятность того, из пяти вызовов а)три закончатся разговором; б) хотя бы четыре закончатся разговором.
Решение.
Пусть событие А - вызов заканчивается разговором. Тогда Р(А) =1-0,1=0,9, а q =0,1. Каждый набор номера является испытанием. Происходит повторение испытаний, в которых вероятность появления события А не зависит от результатов предыдущих испытаний. Поэтому для вычисления вероятностей используем формулу Бернулли.
а) m =3, n =5;
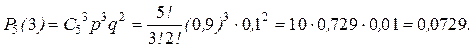
б) "Хотя бы четыре" - это значит 4 или 5.
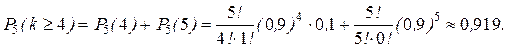
Пример 8. Мини-АТС обслуживает 8 абонентов. Каждый из них занимает соединительную линию с городской телефонной сетью в среднем 12 минут в час. Определить необходимое число линий для практически безотказного обслуживания абонентов.
Решение.
Испытанием является проверка - говорит ли данный абонент (соб. А). Вероятность этого события равна р =12/60=0,2; q =0,8. Проверка повторяется 8 раз. Для ответа на поставленный вопрос по формуле Бернулли вычислим вероятности всех исходов испытаний. Вероятность того, что никто из абонентов не занимает соединительную линию равна
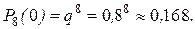
Вероятность того, что разговаривает один абонент равна
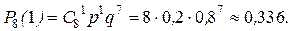
Аналогично
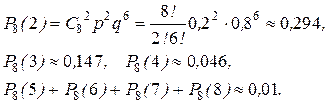
Из расчетов следует, что достаточно иметь 4 линии связи. При этом в среднем только для одного из 100 вызовов не найдется свободной линии.
Пример 9. Из партии, нестандартные изделия в которой составляют 20%, отобрано 400 единиц. Определить вероятность того, что среди отобранных окажется от 60 до 90 нестандартных изделий.
Решение.
По условию p =0,2; q =0,8; n =40; m1 =60; m2 =90.
Воспользуемся интегральной теоремой Лапласа (11):
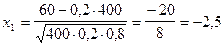
и 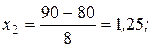
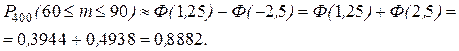
Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Например, поступление вызовов на АТС, последовательность отказов элементов и т.п. Среди большого разнообразия потоков событий выделяют простейший поток событий, который обладает следующими свойствами:
стационарности, т.е. вероятность появления К событий за промежуток времени t есть функция, зависящая только от t и К;
отсутствие последствия, т.е. имеет место взаимная независимость появления числа событий в непересекающиеся промежутки времени;
ординарности, т.е. за бесконечно малый промежуток времени может появиться не более одного события.
Интенсивностью потока 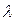 называют среднее число событий, которые появляются в единицу времени.
называют среднее число событий, которые появляются в единицу времени.
Для простейшего потока вероятность появления к событий за время t определяется формулой Пуассона
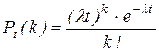 , (12)
, (12)
где 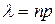 - интенсивность потока.
- интенсивность потока.
Пример 10. АТС получает в среднем 5 вызовов за 1 минуту. Найти вероятность того, что за 2 минуты поступит 8 вызовов.
Решение.
Считая поток вызовов простейшим, по формуле (12) получаем
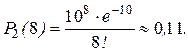
 2015-06-24
2015-06-24 2583
2583